Catchment runoff simulation by coupling data assimilation and machine learning methods
-
摘要: 环境变化影响下流域径流的精确模拟对洪涝灾害防治与区域水资源管理都具有重要意义。在径流模拟研究中, 现有机器学习模型未能充分考虑水文中间状态变量对降雨-径流过程的影响, 本研究基于集合卡尔曼滤波(EnKF)更新水文状态变量, 结合主成分分析(PCA)提取预报因子的主要特征, 采用长短时记忆神经网络(LSTM)构建考虑水文中间变量的机器学习水文模型EnKF-PCA-LSTM。以赣江流域为例, 评估EnKF-PCA-LSTM模型的径流模拟效果, 同时将模拟结果与LSTM模型、物理水文模型HYMOD做对比分析。结果表明, EnKF-PCA-LSTM模型模拟径流的纳什效率系数、Kling-Gupta效率系数和对数纳什效率系数分别为0.954、0.971和0.972, 比LSTM模型和HYMOD模型具有更好的模拟性能, 说明考虑水文状态变量可有效提高机器学习模型的径流模拟精度及稳定性。研究成果可为流域径流模拟提供技术参考。Abstract: Accurate catchment runoff simulation under the changing environment has a great significance in the flood disaster prevention and regional water resources management.The machine learning (ML) approach has been widely and successfully applied in runoff modelling during recent years, which, however, has not yet fully considered the potential impact of changes in hydrological intermediate state variables.This study proposed a coupled ML-based model for runoff simulating by integrating the ensemble Kalman filter (EnKF), the principal component analysis (PCA) and the long short-term memory (LSTM), which denoted as EnKF-PCA-LSTM.The specific steps include: ① The dynamic update of hydrological intermediate state variables via the EnKF method; ② The integration of updated state variables into the input set for predictor selection by the PCA method; ③ Runoff simulation through the combination of chosen predictors with the LSTM model.Taking the Ganjiang River basin as a case study, we provided a comprehensive assessment on the runoff simulation performance of the EnKF-PCA-LSTM, and performed comparisons against that of the original LSTM model and the physical hydrological model HYMOD.Results show that the EnKF-PCA-LSTM outperforms both the LSTM and HYMOD models, as reflected by the higher Nash-Sutcliffe efficiency coefficients, the Kling-Gupta efficiency coefficient and the Nash-Sutcliffe efficiency for the log-transformed runoff (0.954, 0.971 and 0.972, respectively).This finding suggests that considering the hydrological intermediate state could effectively improve the accuracy and stability of ML models in terms of runoff simulation, which undoubtedly provides valuable insight into the catchment runoff modeling.
-
径流模拟是流域水文预报领域非常重要的一环, 也是水文水资源研究中最重要的科学问题之一[1]。近年来, 受强人类活动和全球气候变暖等因素的影响, 极端天气事件频发, 洪涝干旱灾害加剧, 对中国经济和社会造成了极为严重的损失[2-3]。因此, 提出能够适应变化环境的流域径流模拟方法, 从而提高流域径流模拟精度[4], 具有重大的科学意义和实际应用价值。
随着智能监测技术的全面发展, 水文数据更易获取[5], 而利用机器学习方法构建水文输入变量与输出变量的映射关系, 用来开展流域径流模拟成为当前的研究热点之一[6-7]。长短时记忆神经网络(long short-term memory, LSTM)作为热门机器学习方法之一, 在径流模拟领域已经有了广泛的研究和应用[8]。李大洋等[9]提出了基于变分贝叶斯与深度学习的水文概率预报新方法VB-LSTM, 应用于黄河源区流域, 结果表明, VB-LSTM具有一定的灵活性与通用性, 且有效提高了径流预报精度; Khandelwal等[10]将LSTM模型应用到500多个流域, 发现LSTM模型在更多样本数据训练时, 预测结果优于物理机制模型。但目前基于LSTM模型的流域径流模拟预报研究大多是将预测因子直接输入模型[11], 而数据的多源性增加了模型的不确定性, 影响了径流模拟的精准度和计算效率。近期, 李步等[12]将主成分分析(principal component analysis, PCA)与LSTM结合, 构建了融合气象要素时空特征的PCA-LSTM模型, 该方法在黄河源区的应用效果证明了其适用性和鲁棒性。对于流域降雨-径流过程, 水文中间状态变量如土壤湿度、蒸散发等, 对流域径流的形成有着重要影响[11]。因此, 如何提高水文模型对水文中间状态变量的估计, 并将其充分应用到基于机器学习的流域径流模拟中以提高径流模拟精度, 有待进一步研究。
本文将采用集合卡尔曼滤波(ensemble Kalman filter, EnKF)、PCA和LSTM方法构建一种融合数据同化与机器学习的流域径流模拟模型, 记为EnKF-PCA-LSTM, 以赣江流域开展实例研究, 通过同化土壤湿度、蒸散发状态变量, 以期提高机器学习径流模拟精度, 并选取HYMOD水文模型和LSTM模型进行对比分析, 系统评估EnKF-PCA-LSTM模型的流域径流模拟效果。
1 研究方法
1.1 EnKF-PCA-LSTM模型
本文提出的一种融合EnKF、PCA和LSTM的流域径流模拟模型。基于水文气象实测数据, 通过SCE-UA算法[13-14]率定HYMOD水文模型参数的最优值, 以流域历史径流序列, 采用EnKF更新流域水文模型的状态变量, 即实际蒸散发(ET)和土壤湿度(MS); 通过PCA方法进行主成分提取, 得到流域径流模拟因子集合; 根据筛选的径流模拟因子集合和流域实测径流训练LSTM模型, 基于训练好的LSTM模型进行流域径流模拟。
1.1.1 集合卡尔曼滤波
EnKF结合了集合模拟预报的形式和卡尔曼滤波算法, 通过蒙特卡洛方法计算状态变量的预测误差协方差, 将预测值和观测值之间的误差协方差最小化来优化目标估计。主要步骤分为预测和更新, 首先利用状态转移方程对实际问题的状态变量进行预测, 然后根据观测信息和计算得到的增益因子, 更新状态变量[15-16]。
1.1.2 主成分分析
PCA是最常用的线性降维方法之一, 主要步骤是对每一个特征进行去均值处理, 求其协方差矩阵, 再求协方差矩阵的特征值和相对应的特征向量, 选取前k个最大的特征值, 最后将原始特征投影到选取的特征向量上, 得到降维后的k维特征, 以此使用较少的数据维度, 同时保留住较多的原数据点的特性。PCA具体计算步骤可参考文献[17]。当PCA能够提取满足赣江流域径流模拟的因子特征时, 进一步增加主成分阈值对径流模拟影响较小[12], 故本文主成分阈值设为85%。
1.1.3 长短时记忆神经网络
LSTM能够有效捕捉长时序数据之间的关联, 缓解梯度消失或爆炸现象。LSTM的核心结构分为4个部分: 遗忘门、输入门、细胞状态和输出门。其中, 遗忘门决定从之前隐藏层状态中需要舍弃的信息; 输入门选择用哪些新获取的信息更新状态; 细胞状态负责更新记忆单元状态变量, 这也是LSTM有长时间记忆能力的关键; 输出门将部分记忆单元状态变量生成隐藏层状态变量, 形成循环结构。LSTM在水文模拟预报中的详细运算过程可参考文献[18]。
1.1.4 EnKF-PCA-LSTM模型
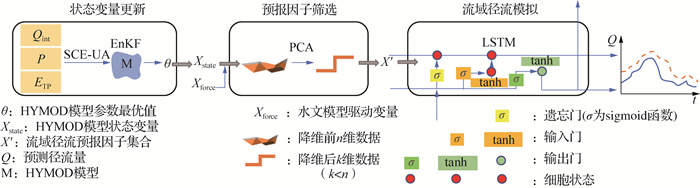
基于以上方法, 本文构建了一种融合EnKF、PCA和LSTM的流域径流模拟模型, 该方法步骤主要包括(图 1):
(1) 将降水(P)、潜在蒸散发(ETP)以及流域出口断面径流(Qint)等作为输入数据; 采用SCE-UA优化算法, 率定得到HYMOD模型参数的最优值, 而后基于HYMOD模型采用EnKF更新状态变量(ET、MS), 更新过程中HYMOD水文模型参数固定不变[19]。
(2) 参考PCA与机器学习结合在水文预报领域的研究[20-21], 将主成分阈值设为85%, 并采用2种方式进行流域径流模拟因子主成分提取: ①针对更新后的状态变量, 结合驱动变量P、Qint, 同时作为输入变量通过PCA进行主成分提取; ②将更新后的状态变量与驱动变量分别采用PCA进行主成分提取。
(3) 将提取得到的主成分输入LSTM模型, 基于流域径流实测资料训练LSTM模型, 最后基于训练好的LSTM模型, 开展流域径流模拟。
1.2 对照模型
为评估EnKF-PCA-LSTM模型的可行性, 本文与LSTM机器学习模型和HYMOD水文模型作对比研究。为验证同化后水文状态变量对径流模拟的影响, LSTM模型的输入变量包括降水、径流、蒸散发和HYMOD模拟得到的未同化处理的土壤湿度。
HYMOD模型是一种基于蓄满产流理论的集总式水文模型, 将一个流域分为无限个不相关联的点的集合, 每一个点都含有一定的初始土壤含水量, 并且该点有其最大蓄水能力(Cmax), 当该点的降水量超过Cmax时, 超出的降水则转为径流。模型的产流计算基于流域蓄水能力曲线[22-23], 公式如下:
$$ F(C)=1-\left(1-\frac{C}{C_{\max }}\right)^B $$ (1) 式中: F(C)为流域内某点蓄水能力累积率; C为流域内某点的蓄水能力, mm; B为流域内某点的蓄水能力空间变化指数。
2 研究区域与数据
2.1 研究区域
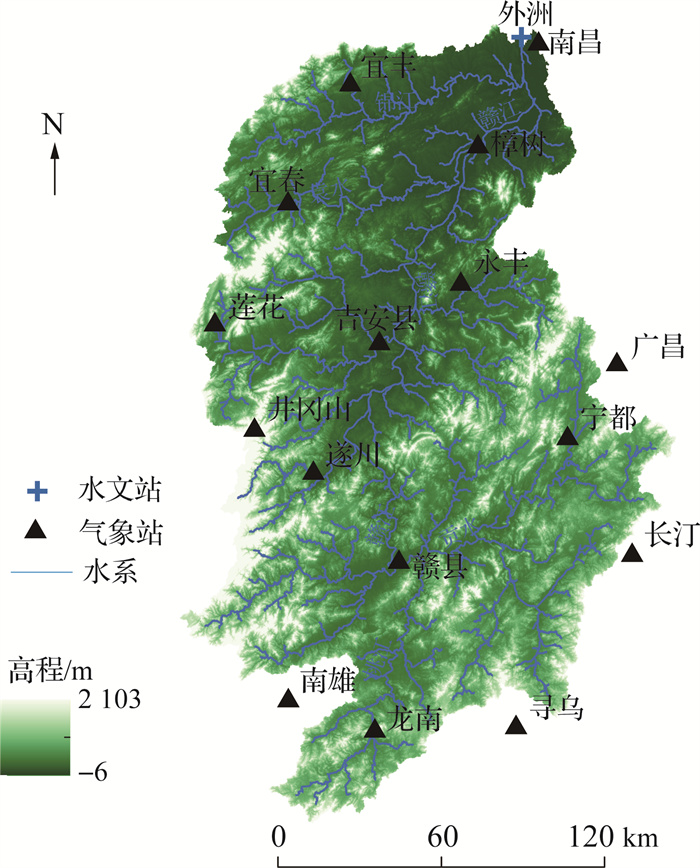
赣江是长江主要支流之一, 为江西省最大河流, 流域面积达81 800 km2。赣江位于长江中下游南岸, 自然落差为937 m, 平均年径流深为849 mm, 平均年径流系数为0.61。流域发源于江西省赣州市石城县洋地乡石寮岽, 地形组成较为复杂, 其中山地、低丘、丘陵分别占流域总面积的44%、31%和21%, 其他为水域和平原。流域汛期为4—9月, 丰枯变化显著, 汛期水量约占全年的73%~78%, 多年平均最大月径流量与最小月径流量比值为5~9[24-25]。
2.2 数据
本文构建模型的输入数据分别为:
(1) Qint来源于水文年鉴外州水文控制站的实测日平均流量数据。
(2) 降水来源于中国气象数据网(http://data.cma.cn/)中赣江流域内及其附近的16个气象站点(如图 2所示)数据。
(3) 蒸散发包括潜在蒸散发和实际蒸散发。潜在蒸散发采用中国气象数据网获取的蒸发皿蒸发数据, 实际蒸散发来源于国家青藏高原科学数据中心(http://data.tpdc.ac.cn/zh-hans/)的遥感反演产品PML-V2[26]。
采用泰森多边形法计算流域面平均降水、面平均蒸发皿蒸发。流域面平均实际蒸散发基于蒸散发产品, 采用Python的GeoPandas库处理得到。由于蒸散发产品PML-V2的起始时间序列为2002-07-04, 故输入数据样本选用2002-07-04/2010-12-31, 并将该段样本数据以7 ∶ 3的比例分为率定期和验证期, 即2002-07-04/2008-06-12为训练期(率定期), 2008-06-13/2010-12-31为测试期(验证期)。
由于模型的预热期导致EnKF同化之后的数据初始阶段误差较大, 为降低对后续模型径流模拟的影响, 同时考虑数据的完整性, 选择2002-07-04/10-04共3个月为预热期。在EnKF更新水文中间状态变量之后, t记为径流模拟当前时刻, t-1为模拟当天的前一日, 则PCA的输入变量为Qt-1、Pt、ET, t和MS, t。
2.3 模型参数设置
(1) EnKF-PCA-LSTM模型。HYMOD水文模型参数的初始值和参考取值范围如表 1所示, 模型参数采用SCE-UA优化算法率定得到; LSTM模型的超参数主要包括隐藏层数(num_layers)、舍弃率(droupout)、迭代次数(epochs)、隐藏神经元数量(hidden_size)、训练批次大小(batch_size)、学习率(learning_size), 超参数的设置也会影响到模型的预测效果和预测时间[27]。本研究参考相关文献并结合前期实验选取参数率定范围[27-28], LSTM模型根据给定的参数率定范围进行多次迭代计算, 并自动输出评价指标Kling-Gupta效率系数最优值对应的一组参数。EnKF-PCA-LSTM模型中LSTM的主要超参数设置如下: num_layers值为1、droupout值为0.15、epochs值为10、hidden_size值为40、batch_size值为32、learning_size值为0.01, 其中num_layers默认设置为1层, 不参与模型参数优选率定过程, 则LSTM模型需要通过参数优选率定的超参数为5个，模型损失函数选取均方根误差(EMS)，模型采用Adam优化器，输入数据采用“Max-Min”归一化方法。
表 1 HYMOD模型参数及取值范围Table 1 Definition of HYMOD model parameters and their ranges模型参数 初始值 最小值 最大值 最大蓄水能力(Cmax) 20 1 500 土壤持水量空间分布指数(B) 0.2 0.1 2 快、慢流速分水系数(α) 0.1 0 0.99 慢速流退水系数(Rs) 0.1 0.1 0.99 三层线性快速流退水系数(Rq) 0.05 0 0.1 (2) 对照模型。为充分证明EnKF-PCA-LSTM模型的可行性, HYMOD模型、LSTM模型的超参数设置与EnKF-PCA-LSTM模型中对应参数设置保持一致。其中, HYMOD模型的输入为流域径流量、面平均降水量和潜在蒸散发量, 输出为土壤湿度和HYMOD模拟径流; LSTM模型的输入为流域径流量、面平均降水量、潜在蒸散发量和HYMOD模型模拟的土壤湿度, 输出为流域径流。同时, 为了检验模型的鲁棒性, 本文采用设置不同标准差的高斯噪音来模拟真实环境中的不确定性[29], 检验EnKF-PCA-LSTM模型是否对作为LSTM模型的输入数据过拟合。
2.4 评价指标
本文采用3个指标评价模型的性能, 分别为纳什效率系数(ENS)、Kling-Gupta效率系数(EKG)和径流对数的纳什效率系数(ENSlnQ)。计算公式分别为:
$$ E_{\mathrm{NS}}=1-\frac{\sum\limits_{t=1}^n\left(Q_{\mathrm{sim}, t}-Q_{\mathrm{obs}, t}\right)^2}{\sum\limits_{t=1}^n\left(Q_{\mathrm{obs}, t}-\overline{Q_{\mathrm{obs}, t}}\right)^2} $$ (2) $$ E_{\mathrm{KG}}=1-\sqrt{(r-1)^2+(\alpha-1)^2+(\beta-1)^2} $$ (3) $$ E_{\mathrm{NSInQ}}=1-\frac{\sum\limits_{t=1}^n\left[\ln \left(Q_{\mathrm{sim}, t}+\zeta\right)-\ln \left(Q_{\mathrm{obs}, t}+\zeta\right)\right]^2}{\sum\limits_{t=1}^n\left[\ln \left(Q_{\mathrm{obs}, t}+\zeta\right)-\overline{\ln \left(Q_{\mathrm{obs}, t}+\zeta\right)}\right]^2} $$ (4) 式中: Qsim, t为t时刻的模型模拟流量; Qobs, t为t时刻的观测流量; $\overline{Q_{\mathrm{obs}, t}}$为观测流量的平均值; r为皮尔逊线性相关系数; α为日径流量模拟值与日径流量观测值标准差的比值; β为模拟日径流量与实测日径流量平均值的比值; n为时间序列的长度; ζ为常数, 用来处理流域特别时段出现的零流量现象, 建议取值为整个时段观测径流平均值的1%[30], 即$\zeta=0.01 \overline{Q_{\text {obs }, t}}$； $\overline{\ln \left(Q_{\text {obs }, t}+\zeta\right)}$为观测流量加上常数ζ后取对数的平均值。
ENS为一个标准化统计指标[31], EKG主要用于对高流量模拟的评估[32], ENSlnQ主要用于评估低流量的模拟效果[30], ENS、EKG和ENSlnQ的取值范围都为(-∞, 1], 取值越接近于1, 说明模型的模拟效果越好, 反之越差。
3 结果与讨论
3.1 PCA 2种方式对比
为了对比在EnKF-PCA-LSTM模型径流模拟过程中数据同化之后, 状态变量与驱动变量同时或分别作为输入变量进行主成分提取的降维结果对最终径流模拟效果的影响, 做如下对比研究。
方案一: 当数据同化之后, 对状态变量与驱动变量分别进行主成分提取, 再将二者的主成分集合作为LSTM的输入数据, 进行径流模拟。
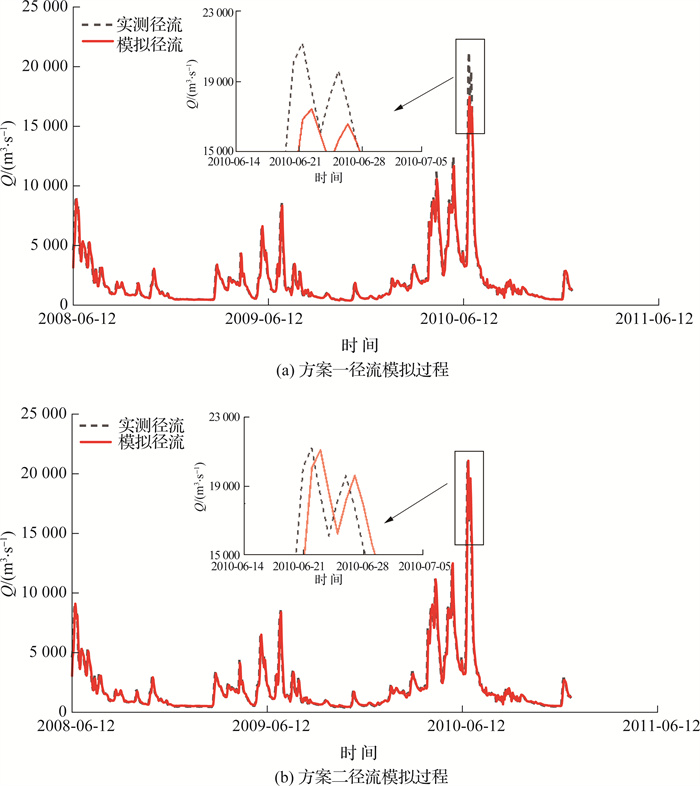
方案二: 将数据同化后的状态变量与驱动变量共同进行主成分提取, 并将主成分集合输入LSTM模型进行模拟, 2种方案的评价指标对比见表 2, 径流模拟结果如图 3所示。
表 2 2种PCA降维方案下径流模拟结果对比Table 2 Comparison of catchment streamflow performances under two PCA dimension reduction scenariosPCA方案 率定期 验证期 ENS EKG ENSlnQ ENS EKG ENSlnQ 方案一 0.948 0.958 0.974 0.951 0.919 0.976 方案二 0.948 0.958 0.970 0.954 0.971 0.974 ![]()
图 3 2种PCA降维方案下径流模拟过程对比Fig. 3 Comparison of simulated and observed streamflow under two PCA dimension reduction scenarios根据表 2所示结果, 在验证期内, 方案二的EKG比方案一高, 其可能的原因是: 方案一进行的2次PCA过程共保留了2个主成分, 这也增加了噪声数据对径流模拟的影响[33], 而方案二进行的PCA过程只保留了1个主成分, 且贡献率约为97%, 相比于方案一在保留输入数据主要特征的同时, 也有效降低了噪声数据的影响。
为了评估PCA在提出方法中的必要性, 本文设置了驱动数据和同化后的状态变量不进行PCA处理的对比方案, 直接作为LSTM的输入数据, 参数设置与方案二保持一致, 结果显示率定期的EKG为0.918, 验证期的EKG为0.916, 其他评价指标也均略低于方案一和方案二。表明采用PCA方法进行主成分提取能够降低噪声数据对径流模拟结果的影响。
在考虑PCA的情景下, 2种方案的ENS和ENSlnQ相差不大, 但在湿润、半湿润地区径流模拟工作中, 一般更关注高流量径流, 因此, 本文采用方案二与HYMOD模型和LSTM模型作以下对比研究。
3.2 不同模型结果对比
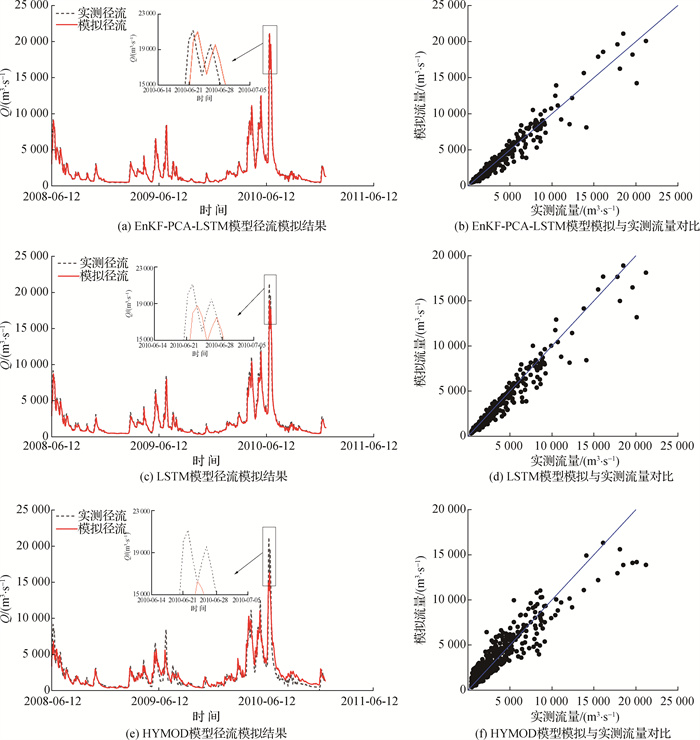
图 4展示了EnKF-PCA-LSTM模型(方案二)与对比模型HYMOD模型和LSTM模型的径流模拟过程, 表 3展示了各模型的评价指标结果。以验证期为例, EnKF-PCA-LSTM、LSTM和HYMOD模型的ENS分别为0.954、0.952和0.841, EKG分别为0.971、0.900和0.849, ENSlnQ分别为0.974、0.972和0.825。结果显示, 3种模型的所有评价指标均大于0.8, 表明3种模型在赣江流域均能取得良好的径流模拟效果。提出的EnKF-PCA-LSTM模型结果最优, LSTM模型次之, 而HYMOD模型最差。相较于对照模型LSTM和HYMOD, EnKF-PCA-LSTM模型径流模拟结果的ENS分别提高了0.2%和13.4%, EKG分别提高了7.9%和14.4%, 而ENSlnQ相较于LSTM模型无提升, 相较于HYMOD模型则提高了17.8%。
![]()
图 4 不同模型模拟径流与实测径流对比Fig. 4 Comparison of observed and simulated streamflow different models表 3 不同模型评价指标对比结果Table 3 Comparison of streamflow performances from different models模型 率定期 验证期 ENS EKG ENSlnQ ENS EKG ENSlnQ EnKF-PCA-LSTM 0.948 0.958 0.970 0.954 0.971 0.974 LSTM 0.943 0.903 0.965 0.952 0.900 0.972 HYMOD 0.790 0.862 0.852 0.841 0.849 0.825 HYMOD模型作为物理过程水文模型, 是对流域真实水文过程的概化, 其刻画的降雨径流过程会存在不足, 导致径流的模拟存在一定的误差。径流过程的高水、低水过程较小的绝对误差亦会产生较大的相对误差, 使得HYMOD模型对于径流过程的总体结果相对较差。LSTM模型是基于数理统计的数据驱动模型[34], 能够基于历史降水、径流等实测数据挖掘更为准确的降雨径流映射关系, 相比于HYMOD模型其径流模拟过程更接近于实测径流, 但LSTM模型本质仍然是基于数据分析建立的映射关系, 未能考虑水文循环过程中的中间变量对径流过程的影响[35-36]。提出的EnKF-PCA-LSTM模型既能充分考虑了水文中间状态变量对径流过程的影响, 也能减少噪声数据, 提高LSTM模型的计算效率, 上述径流模拟结果也验证了该模型在3个模型中表现最优, 特别是在径流过程高水部分的效果提升。
3.3 模型鲁棒性检验
表 4展现了在不同标准差的高斯噪声下, EnKF-PCA-LSTM模型与LSTM模型径流模拟结果的ENS值。结果表明, EnKF-PCA-LSTM模型与LSTM模型对于不同标准差的高斯噪声几乎不受影响, ENS值始终保持在0.94以上, 并且没有发生骤降趋势, 证明了EnKF-PCA-LSTM模型未对作为LSTM模型的输入数据过拟合, 具有很好的鲁棒性。
表 4 EnKF-PCA-LSTM模型与LSTM模型鲁棒性表现Table 4 Robust performance of EnKF-PCA-LSTM model and LSTM model模型 不同标准差下的ENS值 0.03 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20 EnKF-PCA-LSTM 0.954 0.954 0.953 0.953 0.953 0.952 0.952 0.952 0.951 0.951 LSTM 0.952 0.952 0.952 0.951 0.951 0.951 0.950 0.950 0.949 0.949 4 结论
本研究以赣江流域为例, 对比了EnKF-PCA-LSTM模型、LSTM模型和HYMOD模型在日尺度下的径流模拟结果, 主要结论为:
(1) 本研究提出了考虑水文中间状态变量的机器学习模型EnKF-PCA-LSTM, 通过融合集合卡尔曼滤波和主成分分析方法, 不仅考虑了水文状态变量对径流过程的影响, 还减少了输入数据的不确定性, 提高了机器学习模型对径流模拟输入因子有效信息的引入, 可为变化环境下的流域水文模拟提供技术支撑。
(2) 在EnKF-PCA-LSTM模型径流模拟过程中, 经过EnKF同化之后, 状态变量与驱动变量同时作为输入变量进行降维处理, 其最终径流模拟结果要优于状态变量与驱动变量分开降维的结果, 说明并非主成分数量越多, EnKF-PCA-LSTM模型径流模拟效果越好, 过多的主成分数量会增加噪声数据的影响, 削弱主成分分析的降维效果。
(3) 以验证期为例, EnKF-PCA-LSTM模型的Kling-Gupta效率系数对比LSTM模型和HYMOD模型分别提高了7.9%和14.4%; 纳什效率系数和径流对数的纳什效率系数较HYMOOD模型分别提高了13.4%和17.8%, 表明EnKF-PCA-LSTM模型具有很好的适用性和鲁棒性, 模型可提高径流模拟精度, 特别是在高水径流过程。
本文引入EnKF-PCA-LSTM模型的目的在于通过数据同化技术考虑水文中间状态变量的影响, 从而提高流域径流模拟精度。本次研究采用了集总式水文模型, 后续可基于分布式水文模型考虑多维状态变量及下垫面空间异质性对流域产汇流的影响来开展流域径流模拟预报研究。
-
![]()
图 3 2种PCA降维方案下径流模拟过程对比
Fig. 3 Comparison of simulated and observed streamflow under two PCA dimension reduction scenarios
![]()
图 4 不同模型模拟径流与实测径流对比
Fig. 4 Comparison of observed and simulated streamflow different models
表 1 HYMOD模型参数及取值范围
Table 1 Definition of HYMOD model parameters and their ranges
模型参数 初始值 最小值 最大值 最大蓄水能力(Cmax) 20 1 500 土壤持水量空间分布指数(B) 0.2 0.1 2 快、慢流速分水系数(α) 0.1 0 0.99 慢速流退水系数(Rs) 0.1 0.1 0.99 三层线性快速流退水系数(Rq) 0.05 0 0.1 
下载: 导出CSV
表 2 2种PCA降维方案下径流模拟结果对比
Table 2 Comparison of catchment streamflow performances under two PCA dimension reduction scenarios
PCA方案 率定期 验证期 ENS EKG ENSlnQ ENS EKG ENSlnQ 方案一 0.948 0.958 0.974 0.951 0.919 0.976 方案二 0.948 0.958 0.970 0.954 0.971 0.974
下载: 导出CSV
表 3 不同模型评价指标对比结果
Table 3 Comparison of streamflow performances from different models
模型 率定期 验证期 ENS EKG ENSlnQ ENS EKG ENSlnQ EnKF-PCA-LSTM 0.948 0.958 0.970 0.954 0.971 0.974 LSTM 0.943 0.903 0.965 0.952 0.900 0.972 HYMOD 0.790 0.862 0.852 0.841 0.849 0.825
下载: 导出CSV
表 4 EnKF-PCA-LSTM模型与LSTM模型鲁棒性表现
Table 4 Robust performance of EnKF-PCA-LSTM model and LSTM model
模型 不同标准差下的ENS值 0.03 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20 EnKF-PCA-LSTM 0.954 0.954 0.953 0.953 0.953 0.952 0.952 0.952 0.951 0.951 LSTM 0.952 0.952 0.952 0.951 0.951 0.951 0.950 0.950 0.949 0.949
下载: 导出CSV
-
[1] NIU W J, FENG Z K. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management[J]. Sustainable Cities and Society, 2021, 64: 102562. doi: 10.1016/j.scs.2020.102562
[2] 宋晓猛, 张建云, 占车生, 等. 气候变化和人类活动对水文循环影响研究进展[J]. 水利学报, 2013, 44(7): 779-790. SONG X M, ZHANG J Y, ZHAN C S, et al. Review for impacts of climate change and human activities on water cycle[J]. Journal of Hydraulic Engineering, 2013, 44(7): 779-790. (in Chinese)
[3] 张建云, 王银堂, 贺瑞敏, 等. 中国城市洪涝问题及成因分析[J]. 水科学进展, 2016, 27(4): 485-491. doi: 10.14042/j.cnki.32.1309.2016.04.001 ZHANG J Y, WANG Y T, HE R M, et al. Discussion on the urban flood and waterlogging and causes analysis in China[J]. Advances in Water Science, 2016, 27(4): 485-491. (in Chinese) doi: 10.14042/j.cnki.32.1309.2016.04.001
[4] 张海荣. 耦合天气预报的流域短期水文预报方法研究[D]. 武汉: 华中科技大学, 2017. ZHANG H R. Watershed short-term hydrological forecast coupling with weather forecasting[D]. Wuhan: Huazhong University of Science and Technology, 2017. (in Chinese)
[5] 芮孝芳. 水文学与"大数据"[J]. 水利水电科技进展, 2016, 36(3): 1-4. RUI X F. Hydrology and big data[J]. Advances in Science and Technology of Water Resources, 2016, 36(3): 1-4. (in Chinese)
[6] HAO R N, BAI Z X. Comparative study for daily streamflow simulation with different machine learning methods[J]. Water, 2023, 15(6): 1179. doi: 10.3390/w15061179
[7] 董宁澎, 余钟波, 王浩, 等. 耦合水库群参数化方案的区域陆面水文模拟[J]. 水科学进展, 2021, 32(5): 670-682. doi: 10.14042/j.cnki.32.1309.2021.05.003 DONG N P, YU Z B, WANG H, et al. Regional coupled land surface-hydrologic simulation fully coupled with reservoir network scheme[J]. Advances in Water Science, 2021, 32(5): 670-682. (in Chinese) doi: 10.14042/j.cnki.32.1309.2021.05.003
[8] 张力, 王红瑞, 郭琲楠, 等. 基于时序分解与机器学习的非平稳径流序列集成模型与应用[J]. 水科学进展, 2023, 34(1): 42-52. doi: 10.14042/j.cnki.32.1309.2023.01.005 ZHANG L, WANG H R, GUO B N, et al. Integrated model and application of non-stationary runoff based on time series decomposition and machine learning[J]. Advances in Water Science, 2023, 34(1): 42-52. (in Chinese) doi: 10.14042/j.cnki.32.1309.2023.01.005
[9] 李大洋, 姚轶, 梁忠民, 等. 基于变分贝叶斯深度学习的水文概率预报方法[J]. 水科学进展, 2023, 34(1): 33-41. LI D Y, YAO Y, LIANG Z M, et al. Probabilistic hydrological forecasting based on variational Bayesian deep learning[J]. Advances in Water Science, 2023, 34(1): 33-41. (in Chinese)
[10] KHANDELWAL A, XU S M, LI X, et al. Physics guided machine learning methods for hydrology[EB/OL]. [2023-04-29]. https://arxiv.org/abs/2012.02854.pdf.
[11] BHASME P, VAGADIYA J, BHATIA U. Enhancing predictive skills in physically-consistent way: physics informed machine learning for hydrological processes[J]. Journal of Hydrology, 2022, 615: 128618. doi: 10.1016/j.jhydrol.2022.128618
[12] 李步, 田富强, 李钰坤, 等. 融合气象要素时空特征的深度学习水文模型[J]. 水科学进展, 2022, 33(6): 904-913. doi: 10.14042/j.cnki.32.1309.2022.06.005 LI B, TIAN F Q, LI Y K, et al. Development of a spatiotemporal deep-learning-based hydrological model[J]. Advances in Water Science, 2022, 33(6): 904-913. (in Chinese) doi: 10.14042/j.cnki.32.1309.2022.06.005
[13] 王宇晖, 雷晓辉, 蒋云钟, 等. HYMOD模型参数敏感性分析和多目标优化[J]. 水电能源科学, 2010, 28(11): 15-17, 122. doi: 10.3969/j.issn.1000-7709.2010.11.005 WANG Y H, LEI X H, JIANG Y Z, et al. Parameter sensitivity analysis and multi-objective optimization on HYMOD model[J]. Water Resources and Power, 2010, 28(11): 15-17, 122. (in Chinese) doi: 10.3969/j.issn.1000-7709.2010.11.005
[14] DUAN Q Y, GUPTA V K, SOROOSHIAN S. Shuffled complex evolution approach for effective and efficient global minimization[J]. Journal of Optimization Theory and Applications, 1993, 76(3): 501-521. doi: 10.1007/BF00939380
[15] BURGERS G, jan van LEEUWEN P, EVENSEN G. Analysis scheme in the ensemble Kalman filter[J]. Monthly Weather Review, 1998, 126(6): 1719-1724. doi: 10.1175/1520-0493(1998)126<1719:ASITEK>2.0.CO;2
[16] REICHLE R H, MCLAUGHLIN D B, ENTEKHABI D. Hydrologic data assimilation with the ensemble Kalman filter[J]. Monthly Weather Review, 2002, 130(1): 103-114. doi: 10.1175/1520-0493(2002)130<0103:HDAWTE>2.0.CO;2
[17] 朱春苗, 吴海江, 宋小燕, 等. 基于多因子组合的SVR模型在松花江流域径流预报中的应用[J]. 水电能源科学, 2021, 39(6): 12-15, 41. ZHU C M, WU H J, SONG X Y, et al. Application of SVR model based on multi-factors combination in streamflow forecasting of Songhua River basin[J]. Water Resources and Power, 2021, 39(6): 12-15, 41. (in Chinese)
[18] KRATZERT F, KLOTZ D, BRENNER C, et al. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks[J]. Hydrology and Earth System Sciences, 2018, 22(11): 6005-6022. doi: 10.5194/hess-22-6005-2018
[19] 王卫光, 邹佳成, 邓超. 赣江流域多种数据同化方案的径流模拟比较[J]. 湖泊科学, 2023, 35(3): 1047-1056. WANG W G, ZOU J C, DENG C. Comparison of data assimilation based approach for daily streamflow simulation under multiple scenarios in Ganjiang River basin[J]. Journal of Lake Sciences, 2023, 35(3): 1047-1056. (in Chinese)
[20] HUANG S C, LAWRENCE D, IRENE BEOX N, et al. Direct statistical downscaling of monthly streamflow from atmospheric variables in catchments with differing contributions from snowmelt[J]. International Journal of Climatology, 2021, 41(S1): E2757-E2777.
[21] FAN Y R, HUANG G H, LI Y P, et al. Development of PCA-based cluster quantile regression (PCA-CQR) framework for streamflow prediction: application to the Xiangxi River watershed, China[J]. Applied Soft Computing, 2017, 51: 280-293. doi: 10.1016/j.asoc.2016.11.039
[22] MOORE R J. The probability-distributed principle and runoff production at point and basin scales[J]. Hydrological Sciences Journal, 1985, 30(2): 273-297. doi: 10.1080/02626668509490989
[23] 全钟贤, 罗华萍, 孙文超, 等. 概念性水文模型HYMOD在雅砻江流域的适用性研究[J]. 北京师范大学学报(自然科学版), 2014, 50(5): 472-477. QUAN Z X, LUO H P, SUN W C, et al. Application of conceptual hydrological model HYMOD in the Yalong River basin[J]. Journal of Beijing Normal University(Natural Science), 2014, 50(5): 472-477. (in Chinese)
[24] SOLDATOVA E A, SAVICHEV O G, ZHOU D, et al. Ecological-geochemical conditions of surface water and groundwater and estimation of the anthropogenic effect in the basin of the Ganjiang River[J]. Water Resources, 2022, 49(3): 483-492.
[25] 邴建平, 邓鹏鑫, 吴智, 等. 赣江流域生态流量与地表水资源可利用量研究[J]. 人民长江, 2023, 54(2): 127-131, 170. BING J P, DENG P X, WU Z, et al. Ecological flow and available surface water resources in Ganjiang River basin[J]. Yangtze River, 2023, 54(2): 127-131, 170. (in Chinese)
[26] ZHANG Y Q, KONG D D, GAN R, et al. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002—2017[J]. Remote Sensing of Environment, 2019, 222: 165-182.
[27] 殷兆凯, 廖卫红, 王若佳, 等. 基于长短时记忆神经网络(LSTM)的降雨径流模拟及预报[J]. 南水北调与水利科技, 2019, 17(6): 1-9, 27. YIN Z K, LIAO W H, WANG R J, et al. Rainfall-runoff modelling and forecasting based on long short-term memory(LSTM)[J]. South-to-North Water Transfers and Water Science & Technology, 2019, 17(6): 1-9, 27. (in Chinese)
[28] 田远洋, 徐显涛, 彭安帮, 等. 训练数据量对LSTM网络学习性能影响分析[J]. 水文, 2022, 42(1): 29-34, 22. TIAN Y Y, XU X T, PENG A B, et al. Effects of training data on the study performance of LSTM network[J]. Journal of China Hydrology, 2022, 42(1): 29-34, 22. (in Chinese)
[29] KRATZERT F, KLOTZ D, SHALEV G, et al. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets[J]. Hydrology and Earth System Sciences, 2019, 23(12): 5089-5110.
[30] PUSHPALATHA R, PERRIN C, LE MOINE N, et al. A review of efficiency criteria suitable for evaluating low-flow simulations[J]. Journal of Hydrology, 2012, 420/421: 171-182.
[31] NASH J E, SUTCLIFFE J V. River flow forecasting through conceptual models part I: a discussion of principles[J]. Journal of Hydrology, 1970, 10(3): 282-290.
[32] SANTOS L, THIREL G, PERRIN C. Technical note: pitfalls in using log-transformed flows within the KGE criterion[J]. Hydrology and Earth System Sciences, 2018, 22(8): 4583-4591.
[33] 张婧, 刘倩. 主成分分析阈值选择差异性分析研究[J]. 数据采集与处理, 2022, 37(5): 1012-1017. ZHANG J, LIU Q. Difference analysis research of threshold selection in principal component analysis[J]. Journal of Data Acquisition and Processing, 2022, 37(5): 1012-1017. (in Chinese)
[34] LEE J, NOH J. Development of a one-parameter new exponential (ONE) model for simulating rainfall-runoff and comparison with data-driven LSTM model[J]. Water, 2023, 15(6): 1036.
[35] PENG A B, ZHANG X L, XU W, et al. Effects of training data on the learning performance of LSTM network for runoff simulation[J]. Water Resources Management, 2022, 36(7): 2381-2394.
[36] HASHEMI R, BRIGODE P, GARAMBOIS P A, et al. How can we benefit from regime information to make more effective use of long short-term memory (LSTM) runoff models?[J]. Hydrology and Earth System Sciences, 2022, 26(22): 5793-5816.
-
期刊类型引用(12)
1. 邓超，孙培源，尹鑫，邹佳成，王卫光. 基于概念性水文模型与长短时记忆模型耦合的汉江上游流域径流模拟. 湖泊科学. 2025(01): 279-292 . 
百度学术
2. 曹彪，刘敏杰，余其鹰，张廷，马强. 基于PSO-TCN深度学习模型的新疆台兰河流域洪水预报研究. 中国防汛抗旱. 2025(02): 74-80 . 百度学术
3. 袁赛瑜，陈逸鸿，罗霄，张汇明，唐洪武. 知识数据双驱动的感潮河网水动力智能模拟方法. 水科学进展. 2025(01): 28-38 . 本站查看
4. 高玉芳，何川，彭涛，高勇. 降水空间信息的处理策略对径流预测的影响. 水科学进展. 2025(01): 143-154 . 本站查看
5. 黄靖涵，王兆才，吴俊豪，姚之远. 基于深度学习集合优化模型的径流区间预测研究. 水利学报. 2025(02): 240-252+265 . 百度学术
6. 陈泽鑫，赵铜铁钢. 基于可微参数学习的积融雪新安江模型. 水科学进展. 2025(02): 204-216 . 本站查看
7. 赵铜铁钢，张弛，田雨，李昱，陈泽鑫，陈晓宏. 全球气象预报驱动流域水文预报研究进展与展望. 水科学进展. 2024(01): 156-166 . 本站查看
8. 刘成帅，解添宁，李文忠，胡彩虹，徐源浩，牛超杰，余其鹰. 考虑径流过程矢量化的机器学习洪水预报模型. 水科学进展. 2024(03): 420-429 . 本站查看
9. 李成业，彭杨，罗诗琦，于显亮，姚礼双. 基于深度学习的河道非恒定流糙率反演方法. 水力发电学报. 2024(10): 42-52 . 百度学术
10. 冯准，甘新，梁艳. 电信息技术在无线定位系统中的应用研究. 信息记录材料. 2024(11): 39-41+44 . 百度学术
11. 李巧玲，刘兴文，李致家，黎洪德. 多源多层土壤湿度实时同化及在实时洪水预报中的应用. 水科学进展. 2024(05): 773-783 . 本站查看
12. 徐雨妮，许银山，仇红亚，冯志州，惠宇. 鄂东北诸河来水对汉口站水位顶托量化研究. 人民长江. 2024(12): 39-45 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 599
- HTML全文浏览量: 257
- PDF下载量: 254
- 被引次数: 17
