Exploring evapotranspiration characteristics in urbanized areas of Tianjin plain
-
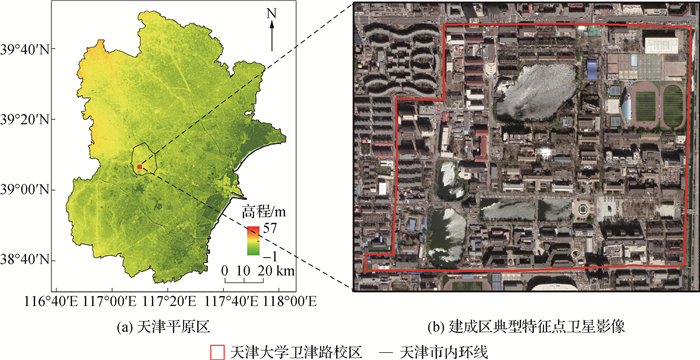
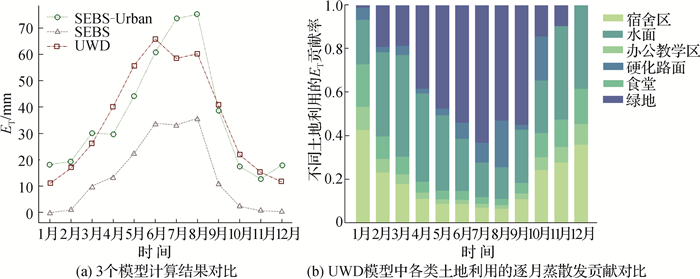
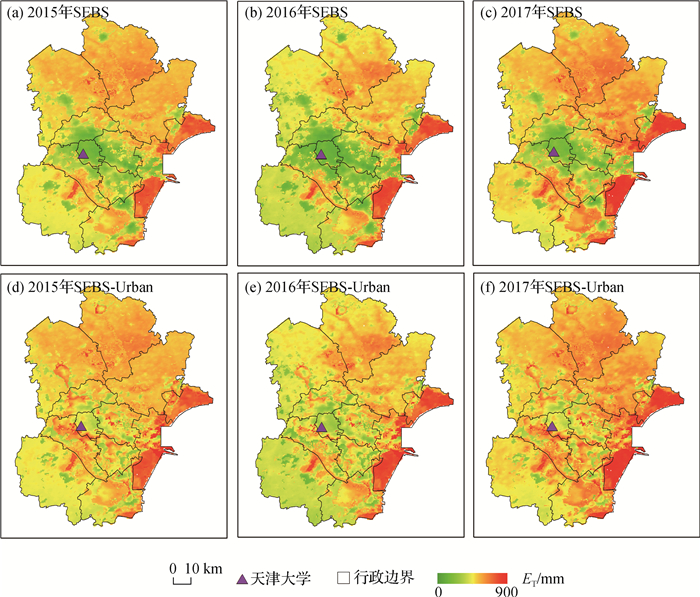
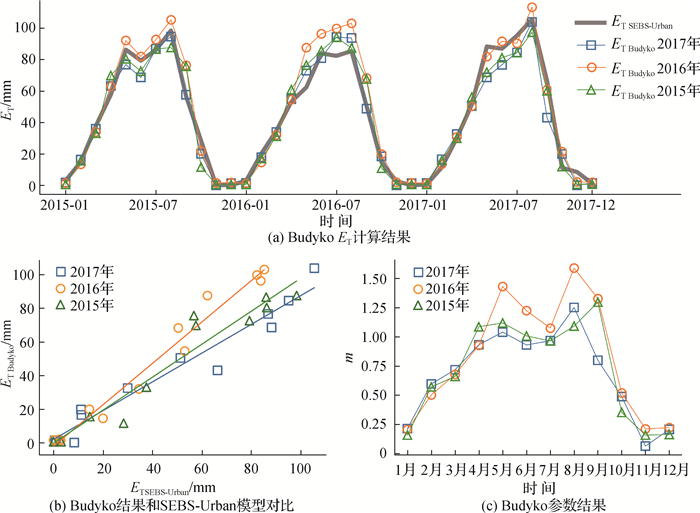
摘要: 为揭示城市蒸散发特征,采用考虑人为热影响的SEBS-Urban模型计算天津平原区2015—2017年逐月蒸散量。使用两步验证法对结果进行检验,首先利用MODIS MOD16产品对非建成区模拟结果合理性进行验证,其次利用城市耗水(UWD)模型得到的天津大学卫津路校区月蒸散量对建成区模拟结果验证。在SEBS-Urban模拟结果基础上,检验Budyko方程在城市化地区的适用性。结果表明:① SEBS-Urban模型精度可靠,体现了蒸散发项在城市地表能量平衡与二元水循环中的相合性;②人为热或社会侧的耗水会导致蒸散发量增加,建成区增幅达85%~115%,整个研究区增幅为7.2%~8.7%;③ Budyko方程在研究区具有较好的拟合效果,可应用于城市地区。本研究成果可为城市化地区蒸散发研究提供必要的参考。
-
关键词:
- 蒸散发 /
- 地表能量平衡 /
- 城市化 /
- SEBS-Urban模型 /
- 城市耗水模型
Abstract: To reveal the characteristics of urban-based evapotranspiration, a SEBS-Urban model was applied to estimate the monthly evapotranspiration(ET) that occurred in the plain area of Tianjin over 2015—2017 considering anthropogenic heat release. A two-step verification method was used. First, a comparative analysis was performed with the MODIS MOD16 products for rural areas. Second, the urban water dissipation (UWD) framework was used to assess the model's performance in built-up areas. The feasibility of the Budyko formula was explored based on the SEBS-Urban results. Three key results were obtained: ① The SEBS-Urban model is reliable, and the results of the built-up area ET analysis are consistent from the perspectives of an urban surface energy balance and a dualistic water cycle. ② The ET increment ranges up to 85%~115% for the built-up area but only 7.2%~8.7% for the whole study area after including considerations for anthropogenic heat. ③ The Budyko formula obtained good results for estimating evapotranspiration in the study area, suggesting that it can also be applied to urban areas. The results of this study can provide a necessary reference for studies on evapotranspiration in urbanized areas.-
Keywords:
- evapotranspiration /
- surface energy balance /
- urbanization /
- SEBS-Urban /
- urban water dissipation
-
水少沙多、水沙关系不协调是黄河下游输水输沙通道不畅的症结所在。1986年以来, 受气候变化与人类活动的共同影响, 黄河流域产水产沙特性呈阶段性变化[1-2], 直接影响下游河道冲淤状态, 河床形态不断调整重塑, 强烈改变了河道过流能力。小浪底枢纽运行前, 黄河下游持续淤积, 主槽萎缩, 过流能力降低, 严重威胁下游防洪安全。小浪底枢纽运行后, 控制了流域90%以上的来沙量[3], 下游主槽实现全线冲刷, 河道输水输沙能力显著提高。进一步研究近30 a来持续淤积与持续冲刷过程中黄河下游河道过流能力的调整规律, 量化汛期与非汛期水沙条件对不同河段平滩流量的影响, 能够更好地理解黄河下游输水输沙通道的动态变化, 为上游水库水沙调控体系的完善与下游河道的防汛安全提供重要参考。
以往学者基于实测水沙数据及断面地形资料, 采用平滩流量、平滩河槽形态、洪水位等各类指标, 对黄河下游河道断面或河段尺度过流能力的调整规律进行了大量研究。平滩流量是代表河道排洪输沙能力的常用指标, 如Hu等[4]、王远见等[5]分别针对黄河下游持续淤积过程与近60 a冲淤过程分析了平滩流量的变化趋势; He[6]提出了采用最大宽度和有效宽度系数计算断面平滩流量的新方法, 分析了断面平滩流量在洪水期的变化特点,这类分析均是基于各水文断面开展的。徐国宾等[7]针对河道持续冲刷过程, 分析了2次调水调沙试验对平滩流量的恢复作用,计算河段平滩流量时采用了河段平均冲淤情况框算法以及上下水文站断面平均法, 不能完全反映河段平滩流量的实际调整情况。刘晓燕等[8]分析了平滩流量对输沙效率和冲刷效率的影响, 提出了恢复与维持黄河下游过流能力的平滩流量标准;胡春宏等[9]则进一步健全了黄河流域水沙平衡的调控指标体系, 综合确定了上中下游的平滩流量阈值, 为保障健康黄河提供重要依据。
此外, 以往学者也分析了不同水沙因子在平滩流量调整过程中发挥的重要作用, 如Zhang等[10]分析了花园口断面平滩流量的时间尺度特征及其对含沙量的滞后响应规律; 余阳等[11]在分析黄河下游游荡段平滩流量变化规律的基础上, 探究了汛期水沙条件以及小浪底水库修建对河段平滩流量的影响; Cheng等[12]则构建了游荡段平滩流量对汛期水沙条件及汛前主槽形态的综合响应关系, 结果表明平滩流量对河道边界条件的变化较汛期水沙条件更为敏感。由此可见, 目前针对黄河下游平滩流量变化的研究, 大部分从定性或定量的角度分析了汛期来水来沙特征变量对过流能力的影响, 但较少考虑在年内水沙分配比例改变的新情势下, 汛期和非汛期来水来沙对河道过流能力调整的综合作用。而且以往研究多集中于特定水文断面或某一局部河段, 较少有针对整个黄河下游长河段的系统分析。
本文采用黄河下游1986—2020年来水来沙数据及沿程91个固定断面的汛后地形资料, 分析汛期与非汛期水流冲刷强度的变化特点, 计算黄河下游各固定断面及河段尺度的平滩流量, 构建过流能力调整对年内不均衡水沙分配的综合响应关系, 进一步量化汛期及非汛期水沙条件对黄河下游不同河型河段过流能力的相对贡献。
1 研究河段概述
1.1 黄河下游河段概况
黄河下游通常指小浪底水库以下的孟津至利津河段, 流域面积为2.3万km2, 河道总长约785 km, 纵比降上陡下缓, 平均为1.2‱。黄河下游沿程设有7个水文站和91个观测断面, 依据河道形态及河床演变特点不同, 结合水文断面位置可将下游进一步划分为游荡段(孟津—高村)、过渡段(高村—艾山)及弯曲段(艾山—利津), 见图 1。各河段分别设有28、28和35个观测断面。游荡段长约275 km, 河道纵比降约1.9‱, 具有河床宽浅、主流摆动不定、滩岸变形较大等特点; 过渡段长约185 km, 河道纵比降约1.2‱, 由于滩岸土体抗冲性较强, 河床较为稳定[13], 但该河段存在平滩流量较小的“驼峰”段, 阻碍河道行洪; 弯曲段长约272 km, 河道纵比降约1.0‱, 两岸堤距较窄, 约0.5~3 km, 该河段有大量险工及控导工程, 长度占河道长度的70%, 故河床最为稳定。
1.2 来水来沙变化特点
黄河以其水少沙多、水沙异源著称, 其径流约60%来自上游地区, 泥沙约90%来自中游土质疏松的黄土高原地区。自1986年以来, 受流域内气候变化及多水库联合调节、水土保持工程和沿黄大量引水等强人类活动影响, 黄河下游沙量呈阶段性变化[14]。基于1986—2020年实测水文年水沙数据, 以花园口水文站为代表, 进入黄河下游的水沙条件见图 2。小浪底枢纽运行以来(2000—2020年), 人类活动的影响进一步增强, 进入黄河下游的年均水量约277亿m3, 较运行前(1986—1999年)略有减少; 但水库拦沙作用导致下游沙量锐减, 小浪底枢纽运行后年均沙量仅1.2亿t, 较运行前减少了83%。水、沙量的年内不均衡分配关系也发生变化, 黄河流域的非汛期为上一年11月至当年6月, 汛期为当年7—10月, 小浪底枢纽运行后, 汛期水量占比由46%减少至39%; 沙量虽仍集中在汛期输送, 但年内分配更加均匀, 汛期沙量占比由81%减少至63%, 非汛期沙量的影响逐渐增大。
1.3 河床冲淤分布
1986—1999年受黄河中游流域侵蚀等影响, 进入黄河下游的沙量较丰, 下游河道经历阶段性淤积过程(图 3(a)), 累计淤积量达23.71亿m3, 至1999年河道平均淤高了1.69 m(较1985年)。从不同河段冲淤分布看, 游荡段淤积强度最大, 累计淤积量占全下游的68%, 过渡段和弯曲段淤积强度相当, 分别占15%和17%。从年内冲淤变化看(图 3(b), 正为淤积,负为冲刷), 黄河下游河段在汛期呈持续淤积态势, 年均淤积量为2.21亿m3; 在非汛期则呈持续冲刷态势, 年均冲刷量为0.52亿m3。
1999年底小浪底水库下闸蓄水, 下游水沙条件再次发生显著变化, 大量泥沙被拦截在水库内, 下游河道经历持续性冲刷过程(图 3(a)), 1999—2020年累计冲刷量达20.01亿m3, 主槽平均高程降低了1.6 m以上[15]。近坝游荡段直接受到下泄水流的强烈冲刷作用, 冲刷强度为3个河段之首, 累计冲刷量占全下游的67%。从年内冲淤变化看(图 3(b)), 黄河下游在汛期和非汛期均处于持续冲刷状态。对于全河段, 汛期年均冲刷量为0.58亿m3, 而非汛期年均冲刷量仍高达0.37亿m3, 对下游河道冲淤演变有一定贡献; 对于游荡段, 非汛期冲刷显著, 年均冲刷量为0.40亿m3, 为汛期的1.68倍。在2000—2002年及2014—2018年等时期, 黄河下游全河段非汛期冲刷量甚至显著大于汛期, 最高达汛期的11.4倍(2017年), 故非汛期来水来沙条件对河床冲淤具有重要影响。
2 汛期与非汛期水流冲刷强度的变化特点
来水来沙条件通常指进口断面的流量、含沙量、历时及各类因素组合, 是河床演变的决定性因素。采用水流冲刷强度这一指标表征来水来沙条件, 汛期与非汛期的水流冲刷强度可表示为:
$$\bar{F}_{\mathrm{f} 1}=\left(\bar{Q}_{1}^{2} / \bar{S}_{1}\right) \times 10^{-4} $$ (1) $$ \bar{F}_{\mathrm{f} 2}=\left(\bar{Q}_{2}^{2} / \bar{S}_{2}\right) \times 10^{-4} $$ (2) 式中: $\bar{F}_{\mathrm{f} 1}、\bar{F}_{\mathrm{f} 2}$分别为汛期和非汛期的平均水流冲刷强度, m9/(kg·s2); $\bar{Q}_{1}$和$\bar{Q}_{2}$分别为进口断面汛期和非汛期的平均流量, m3/s; $ \bar{S}_{1}$和$\bar{S}_{2}$分别为进口断面汛期和非汛期的平均含沙量, kg/m3。式(1)和式(2)既考虑了流量、含沙量及历时的影响, 也考虑了水流动量对河床冲淤变形的影响[16-17]; 此外, 考虑到输沙率与流量之间存在幂函数关系, 其指数约为2, 故式中的流量平方项还可以表征水流的挟沙能力[18-19]。因此, 水流冲刷强度是反映水沙过程对河床形态演变的综合指标[12]。
现有研究表明, 当下泄水沙条件发生变化时, 坝下游河道的河床形态与过流能力不能随之即刻调整, 而是存在一定时间的滞后响应[20]。为考虑前期水沙条件累积的影响, 一般可以采用前n年滑动平均水流冲刷强度作为来水来沙的综合表征因子[21-22]:
$$ \bar{F}_{n \mathrm{f1}}=\frac{1}{n} \sum\limits_{i=1}^{n} \bar{F}_{\mathrm{f1}} $$ (3) $$ \bar{F}_{n \mathrm{f2}}=\frac{1}{n} \sum\limits_{i=1}^{n} \bar{F}_{\mathrm{f} 2} $$ (4) 式中: n为滑动平均的年份; $\bar{F}_{n\mathrm{f1}}、\bar{F}_{n\mathrm{f2}}$分别为汛期和非汛期的前n年平均水流冲刷强度, m9/(kg·s2)。
分别计算各河段1986—2020年汛期及非汛期的前5 a平均水流冲刷强度(图 4), 可见, 黄河下游河道持续淤积过程中, 水流冲刷强度受较大来沙量影响呈现持续减小趋势, 小浪底枢纽运行后的持续冲刷过程中, 各河段水流冲刷强度则因沙量锐减而显著增大。从汛期与非汛期来看, 小浪底枢纽运行后, 游荡段的非汛期水流冲刷强度显著大于汛期, 过渡段的汛期与非汛期水流冲刷强度大小相当, 弯曲段则呈汛期水流冲刷强度大于非汛期的特点。水流冲刷强度越大, 反映水流挟沙能力相较于含沙量越大, 该水沙情势对河床冲刷的影响越大, 故非汛期水流冲刷强度能够对游荡段产生较大影响, 对弯曲段影响则相较更弱。
3 黄河下游过流能力调整规律
3.1 黄河下游平滩流量计算
小浪底枢纽运行前, 黄河下游河槽萎缩严重, 过流能力显著下降; 小浪底枢纽运行后, 受其蓄水拦沙影响, 下游河道持续冲刷, 过流能力恢复。当断面水位与河漫滩基本齐平时, 流量对塑造河床形态的作用最大[23], 故平滩流量是决定河道排洪输沙能力的重要指标。此处采用平滩流量来表征河道过流能力, 在该流量下水流具有最优输沙效率[8]。
计算固定断面平滩流量时, 首先根据黄河下游沿程91个断面的汛后地形资料, 套绘相邻年份各断面的汛后地形, 确定平滩高程; 再采用一维水动力学模型计算各固定断面的水位—流量关系; 最后结合断面平滩高程与计算的水位—流量关系, 确定各固定断面的平滩流量。具体计算过程见文献[24]。然而受固定断面的河槽形态沿程差异较大等影响, 各断面之间的平滩流量差异显著, 特定断面的变化特点无法反映河段整体平滩流量的变化规律[6]。故采用Xia等[25]提出的基于对数转换的几何平均与断面间距加权平均相结合的方法, 进一步计算河段尺度的平滩流量:
$$ \begin{equation*} \bar{Q}_{\mathrm{bf}}=\exp \left[\frac{1}{2 L} \sum\limits_{i=1}^{N-1}\left(\ln Q_{\mathrm{bf}, i+1}+\ln Q_{\mathrm{bf}, i}\right)\left(x_{i+1}-x_{i}\right)\right] \end{equation*} $$ (5) 式中: $\bar{Q}_{\mathrm{bf}}$为河段平滩流量, m3/s; L为河段长度, m; N为河段的固定断面总数; Qbf, i和Qbf, i+1分别为第i个和第i+1个断面的平滩流量, m3/s; xi和xi+1分别为第i个和第i+1个断面与河段起始断面的距离, m。该方法考虑了断面间距不等对计算结果的影响。
3.2 持续淤积与持续冲刷过程中平滩流量的调整规律
根据上述断面及河段尺度的平滩流量计算方法, 计算了黄河下游各固定断面及3个河段的汛后平滩流量。选择3个典型年份, 各固定断面平滩流量沿程变化结果如图 5(a)所示。从时间变化看, 下游河段各断面平滩流量在持续淤积过程中显著减小, 而在持续冲刷过程中得到不同程度的恢复; 从沿程变化看, 游荡段各断面的平滩流量较其他两河段的断面平滩流量更大。尽管黄河下游卡口断面位置在不同年份有所变化, 但卡口河段依然集中在过渡段。1999年过渡段有41%的断面平滩流量小于2 000 m3/s, 其中南小堤断面(距坝317 km)过流能力最小, 平滩流量仅1 100 m3/s; 2020年平滩流量最小的断面位于过渡段路那里断面(距坝446 km), 但平滩流量已显著提升至4 375 m3/s。
3个河段平滩流量的计算结果如图 5(b)所示。从下游河道不同冲淤阶段来看: ①小浪底枢纽运行前, 黄河下游淤积严重, 河床抬高, 各河段平滩流量由1986年的6 000 m3/s降至1999年的2 000~3 000 m3/s,尤其是过渡段平滩流量仅2 339 m3/s, 过流能力持续降低。②小浪底枢纽运行后, 河床沿程持续冲刷下切, 平滩流量呈2个阶梯式不断增加, 2000—2006年为水库拦沙初期, 平滩流量显著提升后趋于稳定, 其中游荡段的过流能力在2005年已恢复至1986年水平; 2007—2020年为水库拦沙后期, 黄河调水调沙正式转入生产应用, 受水沙调控影响, 下游河槽行洪输沙能力再次提升, 近年来过渡段和弯曲段的过流能力也逐渐恢复至1986年水平, 至2020年汛后3个河段的平滩流量已分别达8 713、6 165和6 384 m3/s。
从过流能力的沿程变化来看, 小浪底枢纽运行前各河段过流能力差异不大, 而小浪底枢纽运行后游荡段的过流能力较其余两河段恢复更快。这是水库拦沙作用、河段地理位置与河床边界条件的综合作用所致: ①游荡段最靠近小浪底水库, 直接经受清水冲刷作用, 河道纵比降较大, 故河床下切与展宽显著[13]; ②游荡段中段滩岸多为沙质土壤, 土体抗冲性较弱, 故滩岸极易崩退和展宽[26]; ③游荡段险工及控导工程布设较其余两河段少, 控制作用不强[27], 故该河段冲刷强度剧烈, 河床最易变形。
4 黄河下游水沙条件对过流能力的影响
由上述分析可知, 从水沙量来看, 自1986年以来, 水量大部分在非汛期输送, 沙量虽然仍集中在汛期输送, 但年内分配过程已有所坦化; 从河床冲淤来看, 非汛期水沙下泄造成的河床冲淤强度较大, 尤其是在小浪底枢纽运行后。故非汛期水沙条件对黄河下游河道形态塑造及过流能力具有重要作用。此外, 从汛期与非汛期水沙条件相关性来看, 1986—2020年各河段汛期和非汛期水流冲刷强度之间相关性不强, 决定系数(R2)不超过0.45。故为全面研究黄河下游河道过流能力的调整特点, 需要综合考虑汛期和非汛期水沙条件的影响。
4.1 汛期及非汛期水沙条件的综合影响
综合考虑汛期和非汛期水沙条件累积效应的影响, 构建各河段前n年汛期、非汛期平均水流冲刷强度与平滩流量的幂律关系:
$$ \begin{equation*} \bar{Q}_{\mathrm{bf}}=a \bar{F}_{n \mathrm{fl}}^{k_{1}} \bar{F}_{n 12}^{k_{2}} \end{equation*} $$ (6) 式中: a为平滩流量计算式的系数; k1、k2分别为前n年汛期与非汛期平均水流冲刷强度项的指数。
Wu等[20]、Xia等[25]研究结果表明, 在黄河下游河道形态与前期水沙条件的非线性关系中, 滞后年份通常在3~5 a。采用式(1)和式(2)计算的各年汛期与非汛期水流冲刷强度及式(5)计算的河段平滩流量, 选取不同滑动平均年份n进行多元回归分析。根据计算结果, 当n=5时,游荡段、过渡段和弯曲段平滩流量计算值与实测值的R2均较高, 分别为0.92、0.83和0.72。故采用前5 a平均水流冲刷强度进行计算, 率定各河段平滩流量计算公式中的系数与指数, 结果如表 1所示。
表 1 3个河段平滩流量计算公式中的系数与指数Table 1 Coefficients and indices of the bankfull discharge formulas in three reaches河段 a k1 k2 R2 游荡段 2 732.3 0.112 0.148 0.92 过渡段 1 753.5 0.324 0.035 0.83 弯曲段 2 471.4 0.215 0.042 0.72 率定结果显示, 各河段平滩流量计算公式中的指数k1、k2均大于0, 表明平滩流量与前5 a汛期和非汛期平均水流冲刷强度呈相同变化趋势, 即河床持续淤积过程中, 随着汛期和非汛期平均水流冲刷强度不断减小, 各河段平滩流量均呈减小趋势; 而河床持续冲刷过程中平滩流量则随汛期和非汛期平均水流冲刷强度的增大而增大。下泄水流含沙量减少导致汛期和非汛期平均水流冲刷强度增大(图 4), 造成河床冲深下切, 但指数k1、k2均远小于1, 表明各河段过流能力并不会无限制恢复, 在河床冲刷过程中断面形态及河床组成存在持续的自动调整响应作用, 将延缓河道下切速率, 减缓平滩流量的增幅, 使河流系统朝平衡稳定的方向演变[28]。
分别以式(5)、式(6)的平滩流量结果作为实测值和计算值, 各河段平滩流量的逐年变化如图 6所示。计算值与实测值较为相符, 能够较好地反映实际平滩流量的变化趋势与幅度。采用式(6)的计算误差较小, 平均相对误差(EMR)不超过12%, 表明该式能够较好地反映汛期和非汛期水沙条件累积效应对河道过流能力调整的综合作用。
4.2 汛期及非汛期水沙条件的敏感度分析
在汛期或非汛期水沙条件变化的情况下, 各河段平滩流量调整会做出不同程度的响应。灵敏度分析可以评价各河段过流能力对前5 a汛期、非汛期平均水流冲刷强度的响应程度, 从而对比年内不同时期水沙过程对过流能力的影响强弱。本文采用修正Morris法进行灵敏度分析, 该方法是较常用的灵敏度分析法, 通过对各个自变量参数进行特定步长的微扰动, 判断该变化对因变量的影响程度[29]。对自变量F5f1与F5f2分别以固定步长变化, 定义敏感度判别因子为多次扰动的平均值, 即
$$ \begin{equation*} S=\sum\limits_{i=0}^{m-1} \frac{\left(Y_{i+1}-Y_{i}\right) / Y_{0}}{\left(X_{i+1}-X_{i}\right) / X_{0}} /(m-1)=\sum\limits_{i=0}^{m-1} \frac{\left(Y_{i+1}-Y_{i}\right) / Y_{0}}{\Delta_{i+1}-\Delta_{i}} /(m-1) \end{equation*} $$ (7) 式中: S为自变量$ \bar{F}_{5\mathrm{f1}}$或$ \bar{F}_{5\mathrm{f2}}$的敏感度, 以0.05、0.2和1为界划分不敏感参数、中等敏感参数、敏感参数和高敏感参数; m为扰动总次数; X0和Y0分别为自变量和因变量的初始值; Xi和Yi分别为自变量和因变量第i次变化后的值; Δi和Δi+1分别为第i次和第i+1次扰动相对于初始值的变化百分数, Δi+1-Δi即扰动步长。
采用固定扰动步长为25%, 扰动范围为-75%~75%, 即共进行7次扰动。根据计算结果, 游荡段平滩流量对前5 a汛期、非汛期平均水流冲刷强度的敏感度分别为0.149和0.198, 即游荡段的过流能力对二者都较为敏感, 且对非汛期水沙条件较汛期更为敏感;过渡段分别为0.451和0.046, 弯曲段分别为0.292和0.055, 表明过渡段和弯曲段的过流能力均对汛期水沙条件敏感, 对非汛期水沙条件不太敏感。从水沙过程来看, 汛期来流量较大, 这2个河段床沙的细颗粒组分较多, 含沙量的沿程恢复更显著, 小浪底枢纽运用后过渡段在汛期和非汛期分别冲刷了0.15亿和0.01亿m3/a, 而弯曲段在汛期冲刷了0.19亿m3/a, 非汛期淤积了0.04亿m3/a, 故这2个河段水流对河床的冲刷作用在汛期较非汛期更显著, 如图 4(b)、图 4(c)所示; 从人为影响来看, 非汛期持续时间长达8个月, 受沿程大量引水等人类活动的影响较汛期更大, 实际冲刷能力可能进一步显著削弱。故对于过渡段和弯曲段, 汛期来水来沙对河道形态塑造及过流能力调整的作用较非汛期强。
4.3 汛期及非汛期水沙条件的相对贡献
表 1的率定结果表明, 汛期及非汛期水沙条件对不同河段的相对贡献有所不同。当前5 a汛期与非汛期平均水流冲刷强度的增长幅度相同时, 对于游荡段, 非汛期水沙条件累积效益对过流能力的调整作用较汛期更为显著(k2>k1); 对于过渡段与弯曲段, 汛期水沙条件累积效益的调整作用更为显著(k1>k2)。上述敏感度分析结果也同样表明, 不同河段汛期及非汛期水沙条件对过流能力的影响存在差异。
对数平均迪氏指数法(LMDI法)是量化因子贡献度的有效方法, 该方法通过对研究对象进行加法或乘法分解, 客观定量地识别驱动因子的相对贡献[30]。本文采用LMDI法定量计算汛期及非汛期水沙条件对平滩流量的相对贡献, 通过计算前5 a汛期、非汛期平均水流冲刷强度各自引起的平滩流量变化量与平滩流量总变化量之比, 得到2个影响因素的贡献率。为简化表达, 令$\varphi_{1}=\bar{F}_{n f 1}^{k_{1}}、\varphi_{2}=\bar{F}_{n 2}^{k_{2}}$, 将式(6)写为$\bar{Q}_{\mathrm{bf}}=a \varphi_{1} \varphi_{2}$的形式, 则2个影响因素引起的平滩流量变化分别为:
$$ \Delta \bar{Q}_{\mathrm{bf} 1} =\frac{\bar{Q}_{\mathrm{bf}, t}-\bar{Q}_{\mathrm{bf}, 0}}{\ln \bar{Q}_{\mathrm{bf}, t}-\ln \bar{Q}_{\mathrm{bf}, 0}}\left(\ln \varphi_{1, t}-\ln \varphi_{1, 0}\right) $$ (8) $$ \Delta \bar{Q}_{\mathrm{b} 2} =\frac{\bar{Q}_{\mathrm{bf}, t}-\bar{Q}_{\mathrm{bf}, 0}}{\ln \bar{Q}_{\mathrm{bf}, t}-\ln \bar{Q}_{\mathrm{bf}, 0}}\left(\ln \varphi_{2, t}-\ln \varphi_{2, 0}\right) $$ (9) 式中: $\bar{Q}_{\mathrm{bf}, 0}$和$\bar{Q}_{\mathrm{bf}, t}$分别为基准年和第t年的平滩流量计算值; φ1, 0和φ2, 0分别为汛期和非汛期水沙项($\bar{F}_{n f 1}^{k_{1}}、 \bar{F}_{n 12}^{k_{2}}$)在基准年的计算值; φ1, t和φ2, t分别为汛期和非汛期水沙项在第t年的计算值; $\Delta \bar{Q}_{\mathrm{bf1}} $和$\Delta \bar{Q}_{\mathrm{bf2}} $分别为汛期和非汛期水沙条件变化引起的平滩流量变化, 正值表示使促进, 负值表示使削弱, 两者之和应等于基准年和第t年的平滩流量变化值。故两影响因素对各年平滩流量变化的相对贡献率分别为:
$$ \eta_{1}=\mid \Delta \bar{Q}_{\mathrm{bf} 1}|/\left(\left|\Delta \bar{Q}_{\mathrm{bf} 1}\right|+\left|\Delta \bar{Q}_{\mathrm{br} 2}\right|\right) \times 100 \% $$ (10) $$\eta_{2}=\left|\Delta \bar{Q}_{\mathrm{br} 2}\right| /\left(\left|\Delta \bar{Q}_{\mathrm{bf} 1}\right|+\left|\Delta \bar{Q}_{\mathrm{b} 2}\right|\right) \times 100 \% $$ (11) 式中: η1、η2分别为汛期与非汛期水沙条件对平滩流量的相对贡献率, 两者之和为100%。
采用该方法对各河段平滩流量的逐年变化进行分析, 汛期与非汛期水沙条件的相对贡献率如图 7所示。数值大小表示相对贡献大小, 正、负号分别表示对平滩流量的贡献为促进和削弱。结果表明:
(1) 小浪底枢纽运行前的持续淤积过程中, 各河段的汛期、非汛期水沙条件基本导致平滩流量减小, 其中,游荡段汛期、非汛期水沙条件的年均贡献率分别为64%和36%, 非汛期来水来沙有一定贡献; 过渡段和弯曲段则以汛期水沙条件的贡献为主, 汛期的年均贡献率分别占90%和82%。
(2) 小浪底枢纽运行后的持续冲刷过程中, 各河段的汛期、非汛期水沙条件对平滩流量的作用由削弱转为促进; 非汛期水沙条件的相对贡献在各河段均有所增强, 这是因为小浪底水库的运用改变了黄河下游年内水沙分布, 使非汛期的水沙量占比均增大。
(3) 小浪底枢纽运行后, 非汛期的年均贡献率在游荡段增至53%, 对该河段过流能力的恢复作用显著; 在过渡段和弯曲段则增至13%和21%, 虽略有增长, 但这两河段仍以汛期水沙条件影响为主。非汛期水沙条件对游荡段的贡献较其他两河段更大, 这是受河段地理位置与悬沙沿程恢复综合影响的结果。一方面, 游荡段位于黄河下游河道之首, 直接经受小浪底水库水沙下泄的影响(图 1); 另一方面, 悬沙受床沙补给而沿程恢复, 含沙量向下游增大, 冲刷强度沿程减弱(图 8(a))。二者共同作用导致河床冲淤量在空间上分布不均, 小浪底枢纽运行前后, 非汛期河床冲淤强度均在游荡段最强, 而在其余两河段较弱(图 8(b))。故在对游荡段进行理论计算与河道演变分析时尤其应当考虑非汛期水沙因子, 以提高模拟精度。
5 结论
本文基于黄河下游1986—2020年各水文站实测水沙数据与91个固定断面的地形数据, 计算了断面及河段尺度的平滩流量, 分析了游荡段、过渡段与弯曲段过流能力的调整规律, 探究了汛期及非汛期水沙条件对过流能力的综合作用及相对贡献。主要结论如下:
(1) 小浪底枢纽运行前, 黄河下游河道呈汛期淤积、非汛期冲刷的特点, 整体持续淤积。小浪底枢纽运行后, 水流冲刷强度急剧增大, 河道在汛期与非汛期均持续冲刷, 非汛期冲刷幅度是汛期的64%; 其中游荡段非汛期的水流冲刷强度显著大于汛期, 非汛期河床冲刷量也达到汛期的1.68倍。
(2) 采用一维水动力模型及基于对数转换的几何平均与断面间距加权平均相结合的方法, 计算了断面及河段尺度的平滩流量; 综合考虑汛期与非汛期的水沙累积效应, 构建了各河段平滩流量与前5 a汛期、非汛期平均水流冲刷强度的幂律关系。结果表明,河道持续淤积过程中过流能力不断削弱, 最小平滩流量不到2 000 m3/s, 输水输沙通道不畅; 持续冲刷过程中平滩流量显著增加, 游荡段恢复最迅速, 最小过流能力已恢复至4 375 m3/s; 构建的计算式能较好地反映过流能力随汛期与非汛期水沙分配关系的实际变化。
(3) 采用修正Morris法与LMDI法定量计算了汛期与非汛期水沙条件对平滩流量的影响强弱与相对贡献率, 结果表明,非汛期来水来沙对游荡段过流能力的调整作用显著, 贡献率从小浪底枢纽运行前的36%增至运行后的53%; 对过渡段与弯曲段的影响则不显著, 贡献率不到20%。
-
表 1 SEBS与SEBS-Urban模型对研究区2015—2017年ET计算结果
mm Table 1 Simulation ET results of SEBS vs. SEBS-Urban for study area over 2015—2017
月份 2015年 2016年 2017年 SEBS SEBS-Urban SEBS SEBS-Urban SEBS SEBS-Urban 1月 0.3 3.0 1.5 2.9 -1.5 0.4 2月 11.8 14.6 16.7 20.0 9.8 11.3 3月 35.7 37.5 31.9 34.5 27.5 29.9 4月 55.6 57.5 51.3 53.0 49.9 51.3 5月 83.1 86.2 60.6 62.2 85.2 88.2 6月 75.7 79.2 79.3 83.8 83.1 86.8 7月 80.1 86.0 77.4 82.2 88.2 95.0 8月 92.0 98.3 79.6 85.2 100.2 105.4 9月 51.8 56.7 46.5 50.4 61.4 66.3 10月 25.3 28.3 12.3 14.5 8.9 11.1 11月 -14.3 -12.3 -0.9 2.4 6.2 8.4 12月 -8.6 -5.5 -8.6 -4.7 -1.4 1.0 总量 488.5 529.6 447.4 486.4 517.7 555.1 -
[1] ZHAO J F, LI C, YANG T Y, et al. Estimation of high spatiotemporal resolution actual evapotranspiration by combining the SWH model with the METRIC model[J]. Journal of Hydrology, 2020, 586: 124883. doi: 10.1016/j.jhydrol.2020.124883
[2] 宋晓猛, 张建云, 贺瑞敏, 等. 北京城市洪涝问题与成因分析[J]. 水科学进展, 2019, 30(2): 153-165. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201902001.htm SONG X M, ZHANG J Y, HE R M, et al. Urban flood and waterlogging and causes analysis in Beijing[J]. Advances in Water Science, 2019, 30(2): 153-165. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201902001.htm
[3] 陈似蓝, 刘家宏, 王浩. 城市水资源需求场理论及应用初探[J]. 科学通报, 2016, 61(13): 1428-1435. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201613007.htm CHEN S L, LIU J H, WANG H. Initial research on the theory and application of urban water demand field[J]. Chinese Science Bulletin, 2016, 61(13): 1428-1435. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201613007.htm
[4] GAO X, SUN M, LUAN Q, et al. The spatial and temporal evolution of the actual evapotranspiration based on the remote sensing method in the Loess Plateau[J]. The Science of the Total Environment, 2020, 708: 135111. doi: 10.1016/j.scitotenv.2019.135111
[5] LI F W, CAO R X, ZHAO Y, et al. Remote sensing Penman-Monteith model to estimate catchment evapotranspiration considering the vegetation diversity[J]. Theoretical and Applied Climatology, 2017, 127(1/2): 111-121.
[6] KUMAR V, KHAN S, SHAKTI B, et al. Review of evapotranspiration methodologies[J]. American Journal of Earth Science and Engineering, 2018, 1(2): 72-84.
[7] 张圣微, 张鹏, 张睿, 等. 科尔沁沙地典型区生长季蒸散发估算及其变化特征[J]. 水科学进展, 2018, 29(6): 768-778. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201806002.htm ZHANG S W, ZHANG P, ZHANG R, et al. Estimation of growing season evapotranspiration and its variation in a typical area of Horqin Sandy Land[J]. Advances in Water Science, 2018, 29(6): 768-778. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201806002.htm
[8] LIU X Y, XU J Z, ZHOU X Y, et al. Evaporative fraction and its application in estimating daily evapotranspiration of water-saving irrigated rice field[J]. Journal of Hydrology, 2020, 584: 124317. doi: 10.1016/j.jhydrol.2019.124317
[9] 刘曼晴, 胡德勇, 于琛, 等. 辽河三角洲湿地生长季蒸散量时空格局及影响因素[J]. 生态学报, 2020, 40(2): 701-710. https://www.cnki.com.cn/Article/CJFDTOTAL-STXB202002029.htm LIU M Q, HU D Y, YU C, et al. Temporal and spatial change characteristics of growing season evapotranspiration and its cause analysis in Liaohe River delta wetland, China[J]. Acta Ecologica Sinica, 2020, 40(2): 701-710. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-STXB202002029.htm
[10] 周琳. 北京市城市蒸散发研究[D]. 北京: 清华大学, 2015. ZHOU L. Urban evapotranspiration in Beijing[D]. Beijing: Tsinghua University, 2015. (in Chinese)
[11] NIE W S, ZAITCHIK B F, NI G H, et al. Impacts of anthropogenic heat on summertime rainfall in Beijing[J]. Journal of Hydrometeorology, 2017, 18(3): 693-712. doi: 10.1175/JHM-D-16-0173.1
[12] SAILOR D J. A review of methods for estimating anthropogenic heat and moisture emissions in the urban environment[J]. International Journal of Climatology, 2011, 31(2): 189-199. doi: 10.1002/joc.2106
[13] CONG Z T, SHEN Q N, ZHOU L, et al. Evapotranspiration estimation considering anthropogenic heat based on remote sensing in urban area[J]. Science China Earth Sciences, 2017, 60(4): 659-671. doi: 10.1007/s11430-016-0216-3
[14] FARIDATUL M I, WU B, ZHU X L, et al. Improving remote sensing based evapotranspiration modelling in a heterogeneous urban environment[J]. Journal of Hydrology, 2020, 581: 124405. doi: 10.1016/j.jhydrol.2019.124405
[15] JÄRVI L, GRIMMOND C S B, CHRISTEN A. The surface urban energy and water balance scheme (SUEWS): evaluation in Los Angeles and Vancouver[J]. Journal of Hydrology, 2011, 411(3/4): 219-237. http://www.sciencedirect.com/science/article/pii/S0169204611002362
[16] 周晋军, 刘家宏, 董庆珊, 等. 城市耗水计算模型[J]. 水科学进展, 2017, 28(2): 276-284. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201702013.htm ZHOU J J, LIU J H, DONG Q S, et al. Simulation model for urban water dissipation[J]. Advances in Water Science, 2017, 28(2): 276-284. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201702013.htm
[17] ZHOU J J, LIU J H, YAN D Y, et al. Dissipation of water in urban area, mechanism and modelling with the consideration of anthropogenic impacts: a case study in Xiamen[J]. Journal of Hydrology, 2019, 570: 356-365. doi: 10.1016/j.jhydrol.2018.12.054
[18] 郭生练, 郭家力, 侯雨坤, 等. 基于Budyko假设预测长江流域未来径流量变化[J]. 水科学进展, 2015, 26(2): 151-160. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201502001.htm GUO S L, GUO J L, HOU Y K, et al. Prediction of future runoff change based on Budyko hypothesis in Yangtze River basin[J]. Advances in Water Science, 2015, 26(2): 151-160. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201502001.htm
[19] YU X, YANG H B, LI S E, et al. An improved conceptual model quantifying the effect of climate change and anthropogenic activities on vegetation change in arid regions[J]. Remote Sensing, 2019, 11(18): 2110. doi: 10.3390/rs11182110
[20] YANG W J, WANG Y B, LIU X, et al. Evaluation of the rescaled complementary principle in the estimation of evaporation on the Tibetan Plateau[J]. Science of the Total Environment, 2020, 699: 134367. doi: 10.1016/j.scitotenv.2019.134367
[21] DU C, SUN F, YU J, et al. New interpretation of the role of water balance in an extended Budyko hypothesis in arid regions[J]. Hydrology and Earth System Sciences, 2016, 20(1): 393-409. doi: 10.5194/hess-20-393-2016
[22] HAN S J, HU H P, YANG D W, et al. Irrigation impact on annual water balance of the oases in Tarim Basin, Northwest China[J]. Hydrological Processes, 2011, 25(2): 167-174. doi: 10.1002/hyp.7830
[23] CHEN H, HUO Z L, ZHANG L, et al. New perspective about application of extended Budyko formula in arid irrigation district with shallow groundwater[J]. Journal of Hydrology, 2020, 582: 124496. doi: 10.1016/j.jhydrol.2019.124496
[24] 杨汉波. 流域水热耦合平衡方程推导及其应用[D]. 北京: 清华大学, 2008. YANG H B. Derivation and application of the coupled water-energy balance equation[D]. Beijing: Tsinghua University, 2008. (in Chinese)
[25] WEI H B, ZHANG J E, SINGH S K, et al. Response of hydrological system to urbanization: a case study in Tianjin City, China[J]. Desalination and Water Treatment, 2019, 149: 305-314. doi: 10.5004/dwt.2019.23847
[26] ZHANG S, HUANG G, QI Y J, et al. Impact of urbanization on summer rainfall in Beijing-Tianjin-Hebei metropolis under different climate backgrounds[J]. Theoretical and Applied Climatology, 2018, 133(3): 1093-1106. doi: 10.1007/s00704-017-2225-3
[27] SU Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes[J]. Hydrology and Earth System Sciences, 2002, 6(1): 85-99. doi: 10.5194/hess-6-85-2002
[28] NIE W S, SUN T, NI G H. Spatiotemporal characteristics of anthropogenic heat in an urban environment: a case study of Tsinghua Campus[J]. Building and Environment, 2014, 82: 675-686. doi: 10.1016/j.buildenv.2014.10.011
[29] 舒松, 余柏蒗, 吴健平, 等. 基于夜间灯光数据的城市建成区提取方法评价与应用[J]. 遥感技术与应用, 2011, 26(2): 169-176. https://www.cnki.com.cn/Article/CJFDTOTAL-YGJS201102007.htm SHU S, YU B L, WU J P, et al. Methods for deriving urban built-up area using night-light data: assessment and application[J]. Remote Sensing Technology and Application, 2011, 26(2): 169-176. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YGJS201102007.htm
[30] KARSSENBERG D, SCHMITZ O, SALAMON P, et al. A software framework for construction of process-based stochastic spatio-temporal models and data assimilation[J]. Environmental Modelling & Software, 2010, 25(4): 489-502. http://www.sciencedirect.com/science/article/pii/S1364815209002643
[31] LANDERER F W, SWENSON S C. Accuracy of scaled GRACE terrestrial water storage estimates[J]. Water Resources Research, 2012, 48(4): W04531. http://gji.oxfordjournals.org/external-ref?access_num=10.1029/2011WR011453&link_type=DOI
[32] 杨汉波, 杨大文, 雷志栋, 等. 任意时间尺度上的流域水热耦合平衡方程的推导及验证[J]. 水利学报, 2008, 39(5): 610-617. doi: 10.3321/j.issn:0559-9350.2008.05.015 YANG H B, YANG D W, LEI Z D, et al. Derivation and validation of watershed coupled water-energy balance equation at arbitrary time scale[J]. Journal of Hydraulic Engineering, 2008, 39(5): 610-617. (in Chinese) doi: 10.3321/j.issn:0559-9350.2008.05.015
[33] 姜艳阳, 王文, 周正昊. MODIS MOD16蒸散发产品在中国流域的质量评估[J]. 自然资源学报, 2017, 32(3): 517-528. https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZX201703014.htm JIANG Y Y, WANG W, ZHOU Z H. Evaluation of MODIS MOD16 evapotranspiration product in Chinese river basins[J]. Journal of Natural Resources, 2017, 32(3): 517-528. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZRZX201703014.htm
[34] JAHANGIR M H, ARAST M. Remote sensing products for predicting actual evapotranspiration and water stress footprints under different land cover[J]. Journal of Cleaner Production, 2020, 266: 121818. doi: 10.1016/j.jclepro.2020.121818
[35] 叶红, 张廷斌, 易桂花, 等. 2000-2014年黄河源区ET时空特征及其与气候因子关系[J]. 地理学报, 2018, 73(11): 2117-2134. doi: 10.11821/dlxb201811006 YE H, ZHANG T B, YI G H, et al. Spatio-temporal characteristics of evapotranspiration and its relationship with climate factors in the source region of the Yellow River from 2000 to 2014[J]. Acta Geographica Sinica, 2018, 73(11): 2117-2134. (in Chinese) doi: 10.11821/dlxb201811006
-
期刊类型引用(6)
1. 王大洋,王大刚,莫崇勋,姬明飞,刘少博,杜懿,林泽群. 基于改进水量-能量空间坐标分解法的黄河流域实际蒸散发变化归因分析. 水资源与水工程学报. 2024(03): 18-28 .  百度学术
百度学术
2. 侯雷. 武汉市城市化与水资源协调发展研究. 人民长江. 2023(08): 124-130 .  百度学术
百度学术
3. 徐宗学,李鹏. 城市化水文效应研究进展:机理、方法与应对措施. 水资源保护. 2022(01): 7-17 .  百度学术
百度学术
4. 左其亭. 水科学的核心与纽带——人水关系学. 南水北调与水利科技(中英文). 2022(01): 1-8 .  百度学术
百度学术
5. 王国强,王立波,刘廷玺,薛宝林,段利民. 寒旱区草地不对称增温现象对蒸散发的影响分析. 水科学进展. 2022(04): 627-637 .  本站查看
本站查看
6. 缪贝儿,刘智勇,陈兴荣,蓝欣,陈晓宏,林凯荣. 基于水能分配空间坐标系的流域蒸散变异归因研究. 水利学报. 2022(10): 1229-1239 .  百度学术
百度学术
其他类型引用(3)






 下载:
下载: