Study on long duration comprehensive rainstorm formula based on rainstorm attenuation characteristics in Shanghai
-
摘要: 编制适用于不同历时的综合暴雨公式是协调城市管网排水与区域防洪治涝的重要基础。选用上海市代表雨量站徐家汇站65 a实测雨量资料，建立不同重现期暴雨强度与历时关系，解析暴雨衰减规律，编制单一重现期暴雨公式，结合雨力公式推求适用不同重现期的长历时综合暴雨公式，并推导出暴雨重现期公式。结果表明：不同重现期1~24 h历时暴雨强度均以0.74的衰减指数衰减，据此推求的长历时综合暴雨公式可计算1~24 h任意历时、2~100 a任意重现期的设计暴雨，且平均相对和平均绝对均方根误差分别为1.9%和0.009 mm/min，符合规范要求；暴雨重现期公式可估算1~24 h历时内任意场次暴雨的重现期，高效地服务于城市洪涝防治决策。成果已纳入上海市治涝地方标准，对其他城市具有参考价值。Abstract: The comprehensive rainstorm formula applicable to different durations is an important basis for coordinating urban pipe network drainage and regional flood and waterlogging control. The 65-year monitored rainfall series of Xujiahui meteorological station, which was selected to be the representative rain station of Shanghai City, was collected to establish the relationship between rainstorm intensity and duration in different return periods. The rainstorm attenuation characteristics was revealed to formulate the single rainstorm formula of each return period. The long duration comprehensive rainstorm formula applicable to different return periods was explored with reference to the rain force formula, and the rainfall return period formula was derived. Results show that the rainstorm intensity attenuation index between 1 hour and 24 hours in different return periods are approximately 0.74. The obtained long duration comprehensive rainstorm formula could be used to calculate the design storm of any duration (1-24 hours) and any return period (2-100 years), and the relative and absolute root mean square error of the formula are 1.9% and 0.009 mm/min, which meet the requirements of the criterion, respectively. Also, the rainfall return period formula could be applied to ascertain the return period of any rainfall event between 1 hour and 24 hours so as to serve urban flood prevention and control decision making effectively. Notably, the research achievements have been incorporated into the local standards of waterlogging control in Shanghai City and are of significant reference value to other cities.
-
城市洪涝问题历来是一个非常突出的问题[1], 不仅影响城市居住环境质量, 而且事关城市社会经济的可持续发展[2-3], 是城市发展面临的主要问题, 也是水利、市政等相关部门面临的巨大挑战。针对城市洪涝问题, 水利部门和市政部门关注的侧重点有所不同, 水利部门关注区域性洪涝灾害防御, 市政部门关注城市管网排水[4-5]。两部门采用的设计暴雨量确定方法也不同, 市政部门通常利用3 h以内的年最大暴雨所编制的短历时暴雨强度公式来确定设计暴雨量[6], 水利部门通常对年最大24 h暴雨进行频率分析来确定设计暴雨量。随着城市化进程的加剧, 城市管网排水与区域洪涝灾害防御的相互影响日益凸显, 协同考虑排水、治涝与防洪的相互影响, 已成为系统治水的必由之路, 也是水务一体化的必然之举。由此可见, 编制适用于不同历时的综合暴雨公式对城市实现系统治水至关重要。然而, 基于水利部门与市政部门现有的设计暴雨核定方法很难获得3~24 h的综合暴雨公式。
目前, 国内外对短历时暴雨公式的研究不胜枚举[7-10], 但对长历时暴雨公式的研究屈指可数。国际上更多聚焦暴雨强度-历时-频率(IDF)关系对气候变化的响应研究[11-13], 很少涉足长历时暴雨公式的编制；国内的相关研究主要集中在利用频率曲线推算设计暴雨量, 以及在不考虑暴雨衰减特性的条件下编制暴雨公式。如严方家等[14]、王捷音[15]、郑长陵和史桂菊[16]采用年最大值选样方法, 计算了基于P-Ⅲ频率分布曲线的不同重现期不同长历时的设计暴雨量, 未进一步建立长历时暴雨公式, 限制了成果的直接推广应用；袁婷婷等[17]、唐颖等[18]基于P-Ⅲ分布线型对年最大值法得到的5~1 440 min不同历时的实测暴雨样本进行频率分析, 借助市政部门推荐的短历时暴雨强度公式推导出长历时暴雨公式, 未考虑暴雨衰减规律在不同历时之间的差异性, 精度有待提高。因此, 从暴雨衰减特性出发, 编制适用于不同重现期不同历时的综合暴雨公式迫在眉睫。
本文选取易受风暴潮影响、暴雨内涝风险大的上海市作为研究对象, 在揭示其暴雨衰减规律的基础上建立1~24 h长历时范围的综合暴雨公式。
1 上海市暴雨特点
上海市地处长江三角洲最前缘、长江流域最下游, 境内地势低平、河网密布, 为典型的平原感潮河网地区。上海市属于亚热带季风气候区, 雨量充沛, 年平均降雨量1 191.3 mm, 汛期6—9月降雨量占全年的60%以上。上海地区年均暴雨量约占年均降雨量的50%, 静止锋暴雨、暖区暴雨、低压暴雨、台风暴雨为主要暴雨类型, 约占暴雨总数的83%。静止锋暴雨和台风暴雨的雨时较长、降雨范围广、总雨量大, 而暖区暴雨和低压暴雨虽然雨强大, 但雨时短、降雨范围小。相关研究[19]表明, 长历时、大范围的大暴雨容易造成区域性洪涝灾害, 但暴雨历时一般在24 h以内；短历时强暴雨容易造成局部地区严重积水, 但历时短于1 h的暴雨造成的危害和影响一般不大。加强历时为1~24 h暴雨特点的研究对上海市防灾减灾至关重要。
上海市各区的暴雨频次和强度虽略有差异(总体上中心城区略高于郊区), 但各区气候气象、地形地貌基本一致, 其暴雨特性的差异并不十分显著[20], 且郊区的城市化程度也在不断提高, 各区分别编制暴雨公式意义不大。此外, 以徐家汇站为代表的中心城区各历时年最大雨量, 除了极个别历时略低于其他区, 其余历时均略高于其他区。因此, 选取徐家汇站资料来编制全市统一暴雨公式是偏安全的。
2 上海市暴雨衰减规律
暴雨是比较复杂的自然现象, 但也有一定的规律性。暴雨强度随历时延长而衰减的规律是暴雨的重要规律之一, 一般称之为暴雨强度衰减规律, 其具体表现为: 暴雨历时越短, 雨强衰减程度越小；暴雨历时越长, 雨强衰减程度越大。为了厘清暴雨强度与历时的确切关系, 国内外长期水文气象研究成果建议在双对数纸上点绘不同重现期的暴雨强度—历时关系图, 从而得到一组斜率呈现阶段性变化的折线, 不同历时区间的直线斜率就代表该区间暴雨强度衰减指数。绝大部分地区同一重现期的暴雨强度—历时双对数折线会在t=1 h处出现明显的转折点, 部分地区也会在t=6 h处存在转折点[21], 因此, 可以假设t < 1 h的暴雨衰减指数为n1, 1 h≤t＜6 h时为n2, t≥6 h时为n3, 依据不同时间段的直线斜率确定其暴雨强度衰减指数。
为了探明上海市暴雨衰减规律, 选取上海市徐家汇站1949—2013年实测降雨资料, 统计得到历时分别为5 min、10 min、15 min、20 min、30 min、45 min、60 min、90 min、120 min、180 min、240 min、360 min、720 min、1 440 min的年最大降雨量的逐年系列, 并通过了一致性检验, 不同历时前几位暴雨量与均值关系分析表明, 前3位暴雨量均未超过均值的3倍, 且基于上海市暴雨综合统计参数估算得到的各历时前几位暴雨量的重现期均未超过100 a, 表明不需要进行特大值处理。选用P-Ⅲ型分布曲线, 依据“均值不变”、“频率曲线不交叉”等原则, 采用目估适线法进行频率分析(见图 1和表 1)。由表 1可知, 变差系数(CV)在0.25~0.50之间变化, 没有出现大于0.6的异常情况, 且总体上随历时的增加而增加；CS/CV值取3.50(CS为偏差系数), 符合中国暴雨统计参数的分布特征与变化规律[21]。
![]()
图 1 徐家汇站1949—2013年不同历时年最大降雨量P-Ⅲ分布曲线Fig. 1 P-Ⅲ curve fitting of annual maximum rainstorm in different durations from 1949 to 2013 in Xujiahui station表 1 徐家汇站1949—2013年部分历时年最大降雨量P-Ⅲ分布曲线拟合参数Table 1 Parameters of P-Ⅲ curves of annual maximum rainstorm in different durations from 1949 to 2013 in Xujiahui station参数 10 min 30 min 60 min 180 min 360 min 1 440 min CV 0.28 0.34 0.45 0.46 0.47 0.44 CS 0.98 1.19 1.58 1.62 1.63 1.53 由P-Ⅲ曲线拟合结果计算得到重现期分别为2 a、5 a、10 a、20 a、50 a、100 a的不同历时的设计暴雨量(见表 2)。在双对数坐标里点绘暴雨强度与历时关系图, 据此可得到不同重现期下不同历时区间的暴雨强度衰减指数(见表 3)。
表 2 徐家汇站部分历时不同重现期设计暴雨量统计表mm Table 2 Designed rainstorm in different durations under different return periods in Xujiahui station重现期/a 10 min 60 min 360 min 1 440 min 100 35.0 115.2 186.5 258.9 50 32.5 102.8 165.8 231.6 20 29.0 86.1 138.0 194.9 10 26.1 73.2 116.6 166.3 5 23.0 59.8 94.5 136.6 2 18.1 40.6 63.3 93.9 表 3 上海市不同重现期不同时段暴雨衰减指数统计Table 3 Rainstorm attenuation indexes during different time periods under different return periods in Shanghai City暴雨衰减指数 100 a 50 a 20 a 10 a 5 a 2 a n1 0.34 0.36 0.39 0.43 0.47 0.55 n2 0.73 0.73 0.74 0.74 0.74 0.75 n3 0.76 0.76 0.75 0.74 0.73 0.72 上海市暴雨强度与历时的双对数关系在t=1 h处发生了明显的转折, 而在t=6 h处不明显。此外, 不同重现期的10 min~1 h历时区间的暴雨强度衰减指数n1差异显著, 且呈现随重现期增大而减小的趋势, 在坐标中表现为互不平行的直线簇；而不同重现期的1~24 h历时区间的暴雨强度衰减指数n2在0.73~0.75内变化, n3在0.72~0.76内变化, n2与n3的变化区间基本重合, 均值都为0.74, 在坐标中均呈现出几乎互相平行的直线簇, 绝对值差值在±0.02内, 变幅约±2.7%。因此, 可以确定历时1~24 h的暴雨具有基本一致的衰减规律, 其衰减指数为0.74。
3 上海市长历时暴雨公式
3.1 单一重现期暴雨公式
水利部门常用的长历时暴雨强度公式的一般形式[22]如下:
$$ i = \frac{A}{{{t^n}}} $$ (1) 式中: i为暴雨强度, mm/h；A为雨力, 代表t=1 h的平均雨强, mm/h；n为暴雨强度衰减指数；t为暴雨历时, h。
根据上海市暴雨衰减规律研究成果, n=0.74, 2 a、5 a、10 a、20 a、50 a、100 a重现期的A值分别为40.60 mm/h、59.75 mm/h、73.16 mm/h、86.11 mm/h、102.82 mm/h、115.24 mm/h, 代入式(1)可得到不同重现期的暴雨强度公式。
3.2 综合暴雨公式
由式(1)得出的单一重现期暴雨强度公式未包含暴雨重现期这一重要变量, 不同重现期对应不同的暴雨公式, 不便于实际应用。因此, 借鉴《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》[23]推荐的雨力计算公式, 在公式(1)中引入暴雨重现期变量, 雨力计算公式如下:
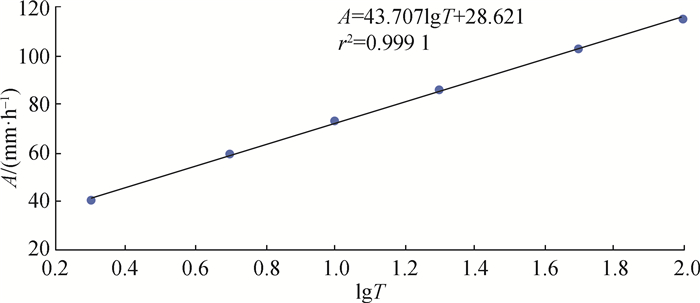
$$ A = {A_1} + C\lg T $$ (2) 式中: A1、C为待求参数；T为重现期, a。
根据不同重现期T对应的A值, 采用最小二乘法拟合得到参数A1=28.621、C=43.707, 确定性系数0.999 1, 拟合结果如图 2所示。
![]()
图 2 上海市暴雨重现期与雨力关系曲线Fig. 2 Relationship between return period and rainfall force in Shanghai City据此, 不同的单一重现期暴雨公式可以统一用综合暴雨公式表达:
$$ i = \frac{{28.621 + 43.7071\lg T}}{{{t^{0.74}}}} $$ (3) 上式等号两侧同乘以历时t, 可得到暴雨量计算公式:
$$ H = \left( {28.621 + 43.7071\lg T} \right){t^{0.26}} $$ (4) 式中: H为暴雨量, mm。
3.3 暴雨公式精度检验
参考《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》[23], 当重现期为2~20 a时, 在一般强度的地方, 平均绝对均方根误差不宜大于0.05 mm/min；在较大强度的地方, 平均相对均方根误差不宜大于5%。本文分别采用平均相对均方根误差和平均绝对均方根误差2项指标来检验推导的长历时综合暴雨公式的精度。经检验[23], 上海市长历时暴雨公式的平均相对均方根误差为1.9%, 平均绝对均方根误差为0.009 mm/min, 均满足暴雨公式编制精度要求。
3.4 暴雨重现期公式
为了便于在实际工作中及时准确地确定实际场次暴雨的重现期, 将式(4)推导为暴雨重现期计算公式:
$$ T = 0.221{\rm{ \times }}10\frac{{0.023H}}{{{t^{0.26}}}} $$ (5) 由式(5)可以确定上海市1~24 h任意历时场次暴雨的重现期。
4 结论
采用上海市徐家汇站1949—2013年实测降雨资料, 确定暴雨强度衰减指数, 结合雨力公式得到上海市长历时综合暴雨公式。主要结论如下:
(1) 不同重现期暴雨呈现的衰减规律一致, 历时1~24 h的暴雨强度衰减指数均约为0.74。
(2) 根据暴雨强度衰减指数和1 h设计暴雨量, 可以编制多个单一重现期的暴雨公式。
(3) 推求得到的长历时综合暴雨公式, 实现了1~24 h任意历时、2~100 a任意重现期的设计暴雨计算公式的统一；由长历时综合暴雨公式推导的暴雨重现期计算公式, 可以估算1~24 h任意历时场次暴雨的重现期。
(4) 编制的长历时综合暴雨公式满足暴雨公式编制的精度要求, 平均相对和平均绝对均方根误差分别仅为1.9%和0.009 mm/min。
本文研制的长历时综合暴雨公式经实践检验是可行的, 已纳入上海市《治涝标准: DB31/T1121—2018》, 对其他城市编制长历时综合暴雨公式具有参考价值。
-
![]()
图 1 徐家汇站1949—2013年不同历时年最大降雨量P-Ⅲ分布曲线
Fig. 1 P-Ⅲ curve fitting of annual maximum rainstorm in different durations from 1949 to 2013 in Xujiahui station
![]()
图 2 上海市暴雨重现期与雨力关系曲线
Fig. 2 Relationship between return period and rainfall force in Shanghai City
表 1 徐家汇站1949—2013年部分历时年最大降雨量P-Ⅲ分布曲线拟合参数
Table 1 Parameters of P-Ⅲ curves of annual maximum rainstorm in different durations from 1949 to 2013 in Xujiahui station
参数 10 min 30 min 60 min 180 min 360 min 1 440 min CV 0.28 0.34 0.45 0.46 0.47 0.44 CS 0.98 1.19 1.58 1.62 1.63 1.53 
下载: 导出CSV
表 2 徐家汇站部分历时不同重现期设计暴雨量统计表
mm Table 2 Designed rainstorm in different durations under different return periods in Xujiahui station
重现期/a 10 min 60 min 360 min 1 440 min 100 35.0 115.2 186.5 258.9 50 32.5 102.8 165.8 231.6 20 29.0 86.1 138.0 194.9 10 26.1 73.2 116.6 166.3 5 23.0 59.8 94.5 136.6 2 18.1 40.6 63.3 93.9
下载: 导出CSV
表 3 上海市不同重现期不同时段暴雨衰减指数统计
Table 3 Rainstorm attenuation indexes during different time periods under different return periods in Shanghai City
暴雨衰减指数 100 a 50 a 20 a 10 a 5 a 2 a n1 0.34 0.36 0.39 0.43 0.47 0.55 n2 0.73 0.73 0.74 0.74 0.74 0.75 n3 0.76 0.76 0.75 0.74 0.73 0.72
下载: 导出CSV
-
[1] 张建云, 王银堂, 贺瑞敏, 等. 中国城市洪涝问题及成因分析[J]. 水科学进展, 2016, 27(4): 485-491. doi: 10.14042/j.cnki.32.1309.2016.04.001 ZHANG J Y, WANG Y T, HE R M, et al. Discussion on the urban flood and waterlogging and causes analysis in China[J]. Advances in Water Science, 2016, 27(4): 485-491. (in Chinese) doi: 10.14042/j.cnki.32.1309.2016.04.001
[2] 胡庆芳, 张建云, 王银堂, 等. 城市化对降水影响的研究综述[J]. 水科学进展, 2018, 29(1): 138-150. doi: 10.14042/j.cnki.32.1309.2018.01.016 HU Q F, ZHANG J Y, WANG Y T, et al. A review of urbanization impact on precipitation[J]. Advances in Water Science, 2018, 29(1): 138-150. (in Chinese) doi: 10.14042/j.cnki.32.1309.2018.01.016
[3] 徐宗学, 陈浩, 任梅芳. 中国城市洪涝致灾机理与风险评估研究进展[J]. 水科学进展, 2020, 31(5): 713-724. doi: 10.14042/j.cnki.32.1309.2020.05.008 XU Z X, CHEN H, REN M F. Progress on disaster mechanism and risk assessment of urban flood/waterlogging disasters in China[J]. Advances in Water Science, 2020, 31(5): 713-724. (in Chinese) doi: 10.14042/j.cnki.32.1309.2020.05.008
[4] 陈子燊, 高时友, 李鸿皓. 基于二次重现期的城市两级排涝标准衔接的设计暴雨[J]. 水科学进展, 2017, 28(3): 382-389. https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201703008.htm CHEN Z S, GAO S Y, LI H H. Design storm for mixed level-1 and level-2 urban drainage standards based on the secondary return period[J]. Advances in Water Science, 2017, 28(3): 382-389. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SKXJ201703008.htm
[5] 贾卫红, 李琼芳. 上海市排水标准与除涝标准衔接研究[J]. 中国给水排水, 2015, 31(15): 122-126. https://www.cnki.com.cn/Article/CJFDTOTAL-GSPS201515033.htm JIA W H, LI Q F. Study on linkage between drainage standards and waterlogging control standards in Shanghai[J]. China Water & Wastewater, 2015, 31(15): 122-126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GSPS201515033.htm
[6] 熊立华, 闫磊, 李凌琪, 等. 变化环境对城市暴雨及排水系统影响研究进展[J]. 水科学进展, 2017, 28(6): 930-942. doi: 10.14042/j.cnki.32.1309.2017.06.014 XIONG L H, YAN L, LI L Q, et al. Advances in analysis of impacts of changing environments on extreme urban rainfall and drainage infrastructure[J]. Advances in Water Science, 2017, 28(6): 930-942. (in Chinese) doi: 10.14042/j.cnki.32.1309.2017.06.014
[7] 刘俊, 周宏, 鲁春辉, 等. 城市暴雨强度公式研究进展与述评[J]. 水科学进展, 2018, 29(6): 898-910. doi: 10.14042/j.cnki.32.1309.2018.06.015 LIU J, ZHOU H, LU C H, et al. A review on recent advances of urban rainfall intensity-duration-frequency relationships[J]. Advances in Water Science, 2018, 29(6): 898-910. (in Chinese) doi: 10.14042/j.cnki.32.1309.2018.06.015
[8] SHAO D N, LIU G S. Up-to-date urban rainstorm intensity formulas considering spatial diversity in China[J]. Environmental Earth Sciences, 2018, 77(14): 541. doi: 10.1007/s12665-018-7718-6
[9] CHANG K B, LAI S H, OTHMAN F. Comparison of annual maximum and partial duration series for derivation of rainfall intensity-duration-frequency relationships in Peninsular Malaysia[J]. Journal of Hydrologic Engineering, 2016, 21(1): 05015013. doi: 10.1061/(ASCE)HE.1943-5584.0001262
[10] 梅超, 刘家宏, 王浩, 等. 城市设计暴雨研究综述[J]. 科学通报, 2017, 62(33): 3873-3884. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201733013.htm MEI C, LIU J H, WANG H, et al. Review on urban design rainstorm[J]. Chinese Science Bulletin, 2017, 62(33): 3873-3884. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201733013.htm
[11] LIMA C H R, KWON H H, KIM J Y. A Bayesian beta distribution model for estimating rainfall IDF curves in a changing climate[J]. Journal of Hydrology, 2016, 540: 744-756. doi: 10.1016/j.jhydrol.2016.06.062
[12] SHAHABUL ALMA M, ELSHORBAGY A. Quantification of the climate change-induced variations in intensity-duration-frequency curves in the Canadian Prairies[J]. Journal of Hydrology, 2015, 527: 990-1005. doi: 10.1016/j.jhydrol.2015.05.059
[13] CHENG L Y, AGHAKOUCHAK A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate[J]. Scientific Reports, 2015, 4: 7093. doi: 10.1038/srep07093
[14] 刘淼, 周荣, 辛朋磊, 等. 南通城市设计暴雨方法比较及公式修订[J]. 水文, 2019, 39(4): 24-28. https://www.cnki.com.cn/Article/CJFDTOTAL-SWZZ201904005.htm LIU M, ZHOU R, XIN P L, et al. Comparison of design rainstorm method and formula revision for Nantong City[J]. Journal of China Hydrology, 2019, 39(4): 24-28. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWZZ201904005.htm
[15] 王捷音. 菏泽市城区长历时暴雨设计[J]. 治淮, 2012(2): 9-10. doi: 10.3969/j.issn.1001-9243.2012.02.004 WANG J Y. Long duration designed rainstorm on Heze City[J]. Harnessing the Huaihe River, 2012(2): 9-10. (in Chinese) doi: 10.3969/j.issn.1001-9243.2012.02.004
[16] 郑长陵, 史桂菊. 新安水文站长历时暴雨量频率分析[J]. 科技创新导报, 2012, 9(15): 224. doi: 10.3969/j.issn.1674-098X.2012.15.188 ZHENG C L, SHI G J. Frequency analysis of long duration rainstorm in Xin'an hydrologic station[J]. Science and Technology Innovation Herald, 2012, 9(15): 224. (in Chinese) doi: 10.3969/j.issn.1674-098X.2012.15.188
[17] 袁婷婷, 李国芳, 王艺晗. 常州市区设计暴雨公式及雨型研究[J]. 水电能源科学, 2019, 37(6): 16-18, 131. https://www.cnki.com.cn/Article/CJFDTOTAL-SDNY201906005.htm YUAN T T, LI G F, WANG Y H. Study on design rainstorm formula and rainstorm pattern in Changzhou urban area[J]. Water Resources and Power, 2019, 37(6): 16-18, 131. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDNY201906005.htm
[18] 唐颖, 周玉文, 赵见, 等. 长历时暴雨强度公式的推求方法[J]. 河北工业科技, 2014, 31(5): 378-383. https://www.cnki.com.cn/Article/CJFDTOTAL-HBGY201405004.htm TANG Y, ZHOU Y W, ZHAO J, et al. Derivation method for long-duration storm intensity formula[J]. Hebei Journal of Industrial Science & Technology, 2014, 31(5): 378-383. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBGY201405004.htm
[19] 李海宏, 王强, 孙一, 等. 近10年上海地区致灾暴雨特征分析[C]//第35届中国气象学会年会S1灾害天气监测、分析与预报. 合肥: 中国气象学会, 2018: 769-783. LI H H, WANG Q, SUN Y, et al. Analysis on the characteristics of catastrophic rainstorm in Shanghai in recent 10 years[C]//Proceedings of the 35th Annual Meeting of the China Meteorological Society S1 Disaster Weather Monitoring, Analysis And Forecast. Hefei: Chinese Meteorological Society, 2018: 769-783. (in Chinese)
[20] 孙兰东, 徐家良. 上海市长历时暴雨强度公式研究[C]//第34届中国气象学会年会S2副热带季风与极端天气气候事件论文集. 郑州: 中国气象学会, 2017: 159-161. SUN L D, XU J L. Study on the long duration rainstorm intensity formula of Shanghai City[C]//Proceedings of the 34th Annual Meeting of the China Meteorological Society S2 Subtropical Monsoon And Extreme Weather Climate Events. Zhengzhou: Chinese Meteorological Society, 2017: 159-161. (in Chinese)
[21] 水利部水文局, 南京水利科学研究院. 中国暴雨统计参数图集[M]. 北京: 中国水利水电出版社, 2006. Hydrology Bureau of Ministry of Water Resources, Nanjing Hydraulic Research Institute. Atlas of storm statistics in China[M]. Beijing: China Water Power Press, 2006. (in Chinese)
[22] 梁忠民, 钟平安, 华家鹏. 水文水利计算[M]. 2版. 北京: 中国水利水电出版社, 2008: 102-104. LIANG Z M, ZHONG P A, HUA J P. Hydrology and water conservation calculations[M]. 2nd th. Beijing: China Water Power Press, 2008: 102-104. (in Chinese)
[23] 住房和城乡建设部, 中国气象局. 城市暴雨强度公式编制和设计暴雨雨型确定技术导则[R]. 北京: 住房和城乡建设部, 中国气象局, 2014. Ministry of Housing and Urban-rural Development, China Meteorological Administration. Technical guidelines for the calculation of urban rainstorm intensity formulation and the determination of rainstorm patter[R]. Beijing: Ministry of Housing and Urban-rural Development, China Meteorological Administration, 2014. (in Chinese)
-
期刊类型引用(8)
1. 任泽凌，李彬权，王国庆，刘加进，鲍振鑫，刘翠善，张磊磊. 城市暴雨强度公式复核——以杭州主城区为例. 南水北调与水利科技(中英文). 2024(01): 80-89 . 
百度学术
2. 和鹏飞，赖瑞勋，许树洪，张晓丽，张馨文. 基于暴雨衰减特性的江苏镇江市综合暴雨公式研究. 中国防汛抗旱. 2024(08): 37-41+80 . 百度学术
3. 刘自香，任东. 黑河流域暴雨递减指数分析. 甘肃水利水电技术. 2023(09): 1-4 . 百度学术
4. 周荣，吴艳鸣，田立，沈建，黄智勇，杨逸，郁昱. 南通市城市暴雨强度公式及设计雨型研究. 科学技术创新. 2022(10): 114-118 . 百度学术
5. 张金良，盖永岗，李超群，沈洁. 洪水递减指数及其在洪水过程设计中的应用研究. 水文. 2022(03): 8-13 . 百度学术
6. 钱真，孔令婷，陈长太，贾卫红. 城市平原感潮河网地区涉河工程防洪影响计算方法研究. 水利规划与设计. 2022(09): 41-45 . 百度学术
7. 李琼芳，许树洪，周正模，和鹏飞，杜尧，虞美秀，陈启慧. 基于系统微分响应的暴雨强度公式参数优化. 水资源保护. 2022(05): 8-16 . 百度学术
8. 张金萍，张航，方宏远，杨锋. 郑州城市暴雨特性研究. 水文. 2021(05): 78-83 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 701
- HTML全文浏览量: 119
- PDF下载量: 147
- 被引次数: 8
